Що таке розподіл
Як влаштовані випадковості.
Число, що випало на гральному кубику, вік перехожого, час очікування літака — це випадкові величини. У роботі ми також зіштовхуємось із ними. Скільки людей сьогодні зайде на сайт, який дохід отримає компанія цього місяця — цього не може бути відомо заздалегідь.
У теорії ймовірностей випадкова величина — це змінна, яка може приймати набір можливих значень, залежно від випадку.
Розподіл імовірностей — це закон, що описує значення випадкової величини та ймовірності їхньої появи.
Насправді випадкові величини часто складно влаштовані. Але в математиці вдалося визначити закономірності їхньої поведінки. Розповідаємо про основні.
Рівномірний розподіл
Класичний приклад — підкидання монетки. Це випадкова величина з двома наслідками — орел або решка. Вважатимемо, що можливість отримати орла чи решку однакова й дорівнює 1/2.
Тепер розглянемо шестигранний гральний кубик. Число, що випало на ньому, — це випадкова величина, що приймає значення від 1 до 6, кожне з ймовірністю 1/6.
Подібний закон спрацює й тоді, якщо ми виберемо довільну цифру, наприклад, у лотерейному білеті. Ми приходимо до випадкової величини, що набирає десять різних значень (від 0 до 9 з кроком 1), кожне з ймовірністю 1/10.
У загальному випадку візьмемо довільне число результатів. Ми приходимо до випадкової величини, що набирає n значень {1,2,3,…, n}, кожне з ймовірністю 1/n. Такий розподіл називається дискретним рівномірним розподілом. Його функція ймовірності незалежно від конкретного значення дорівнюватиме:
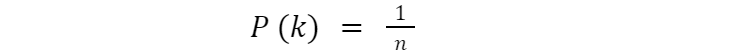
Графік такої функції ймовірностей на деякому відрізку [a, b] буде виглядати так:
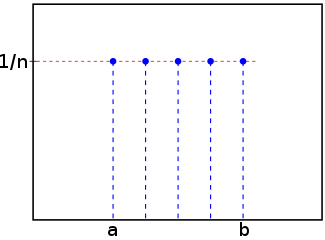
Джерело: Wikipedia
Крім функції ймовірності, з випадковою величиною пов’язують ще один об’єкт. Щоби дізнатися, з якою ймовірністю значення випадкової величини буде менше чи більше якогось числа, використовується функція розподілу. Це ймовірність, що випадкова величина буде меншою або дорівнює довільному значенню, P(Xk). Імовірність серед об’єктів {1,…, n} отримати значення, менше або рівне k, дорівнюватиме k/n. Так ми отримуємо функцію розподілу F(k)=k/n.
Ось її графік:
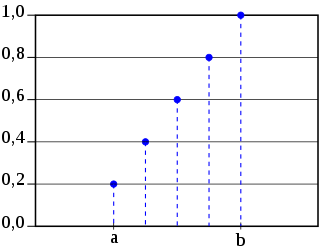
Джерело: Wikipedia
У дискретній моделі число можливих значень випадкової величини скінченне. Розглянемо завдання із безперервним розподілом. Людина потрапляє на залізничну платформу рівноймовірно в довільний момент часу. На цю платформу кожні 30 хвилин приходить поїзд. Слід зрозуміти, яка ймовірність очікування поїзда понад 20 хвилин.
Таке завдання призводить до поняття безперервного рівномірного розподілу. Тут очікування поїзда — випадкова величина, яка набуватиме значення на відрізку від 0 до 30. Імовірність отримати будь-яке чисельне значення на проміжку від 0 до 30 — постійна. Отже, щільність розподілу буде константою. Ця константа має бути такою, щоби площа під графіком щільності дорівнювала одиниці.
У нашому випадку щільність ймовірності дорівнюватиме 1/30. У загальному випадку — 1/(b-a).
Графік:
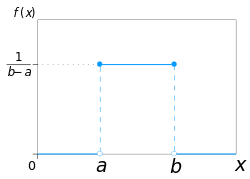
Джерело: Wikipedia
Функція розподілу F(x) — це ймовірність очікування поїзда від a до x хвилин. Вона знаходиться як площа під графіком від а до x функції густини f. Це буде F(x)=x/30, а загальному випадку F(x)=(x-a)/(b-a).
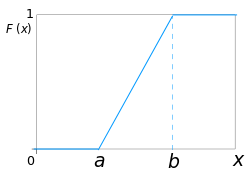
Джерело: Wikipedia
Як бачимо, функція розподілу — це інтеграл від густини розподілу.
Щоби розв’язати завдання, потрібно підрахувати значення P(x>20). Його можна знайти як площу прямокутника із шириною 10 (від 20 до 30) та висотою 1/30. Його також можна визначити як значення 1-F(20). І в тому, і в іншому випадку відповідь буде ⅓. Імовірність прочекати понад 20 хвилин становитиме ⅓.
Усі значення рівномірного розподілу в заданому діапазоні рівноймовірні.
Розподіл Бернуллі
Говорити про рівномірний розподіл ми почали з класичного експерименту з монеткою.Там ймовірність обох результатів була однаковою. А якщо розглянути монету, яка падатиме орлом із ймовірністю p, і решкою — з ймовірністю q?
Нехай випадкова величина з 2 наслідками приймає значення 1 з ймовірністю p і значення 0 c ймовірністю q так, що p+q=1.
Такий розподіл можна застосовувати і в житті. Якщо ви добре підготувалися, то можливість скласти іспит більша, ніж завалити. Досвідчений стрілець із більшою ймовірністю потрапить у ціль, ніж промахнеться.
Ось функція ймовірностей такого розподілу:
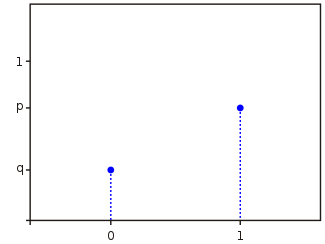
Джерело: Wikipedia
У випадкової величини 2 значення — 0 і 1. Однак її функція розподілу визначається для всіх дійсних чисел:
Значення менше нуля у випадкової величини не вийде ніколи — вона приймає тільки 0 і 1. F(x)=0 для всіх x<0.
Значення 0 буде ймовірністю q за визначенням. F(0)=q.
Знайдемо F(x)=P(X<x) для 0<x<1. Значення 0<x<1 випадкова величина не набуває. Єдине значення, яке менше таких x — це 0. Отже, ймовірність P(X<x) для 0<x<1 — це P(X=0). Тоді F(x) для будь-якого 0<x<1 — це F(0) : F(x)=F(0)=q.
Знайдемо ймовірність отримати значення, менше або рівне 1. Оскільки випадкова величина набуває всього 2 значення й обидва з них <=1, то ця ймовірність дорівнюватиме 1: P(X<=1)=P(X=0 или X=1)=1.
Те саме стосується будь-якого x>1 : P(x)=P(1)=1.
Графік F(x):
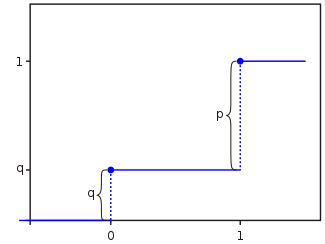
Джерело: Wikipedia
Біноміальний розподіл
Трапляється, що розглядається не одне випробування, а кілька поспіль.
Случается, что рассматривается не одно испытание, а несколько подряд.
Наприклад, колегія лікарів вирішує, чи хворий пацієнт. Два лікарі вважають, що так, а один — що ні.
Модель телефона може містити різні недоліки. Під час огляду з’ясувалося, що в одного телефона дефекти є в дисплея та акумулятора, а в іншого — лише в акумулятора
Оцінимо ймовірність таких подій. Припустимо, що ймовірність події однакова всередині серії. Так, припустимо, що з однаковою ймовірністю p кожен із лікарів ухвалить позитивне рішення. Імовірність дефектів у новому телефоні однакова.
У цих прикладах проводиться серія експериментів Бернуллі: є n експериментів, у кожному з яких ймовірність успіху дорівнює p, ймовірність невдачі — q. Як оцінити ймовірність, що в n випробуваннях буде рівно k успіхів?
Розглянемо випадок із 3 випробувань і знайдемо ймовірність отримати 2 успіхи з 3. Якщо p — ймовірність успіху, а q — ймовірність невдачі, то ймовірності різних комбінацій у цих експериментах будуть такими:
Ймовірність 3 успіхів у 3 випробуваннях =ppp=p3
Ймовірність успіхів у 1-му та 2-му випробуванню та невдачі в 3-му = ppq=p2q
Імовірність успіхів у 1-му та 3-му випробуванні та невдачі у 2-му = pqp=p2q
Імовірність успіху у 1-му випробуванні та невдач у 2-му и 3-му = pqq=q2p
Імовірність невдачі у 1-му випробуванні та успіхів у 2-му и 3-му = qpp=p2q
Імовірність невдачі у 1-му и 3-му випробуванні та успіху у 2-му = qpq=q2p
Вероятность неудачи в 1-му и 2-му випробуванні та успіху в 3-му = qqp=q2p
Імовірність 3 невдач у 3 випробуваннях =qqq=q3
Нас цікавлять випадки 2 успіхів та 1 невдачі. Таких випадків 3 і ймовірність кожного p2q. Вони відрізняються лише тим, у яких саме з трьох експериментів відбулося два успіхи, а в якому — невдача.
Отже, ймовірність 2 успіхів із 3 є 3p2q.
Те, що коефіцієнт дорівнює 3, невипадково. Цю кількість варіантів здобути рівно 2 успіхи в 3 експериментах, тобто вибрати 2 місця з 3 можливих. Число способів вибрати 2 об’єкти з 3 — це число поєднань C23 =3
У загальному випадку число способів вибрати k об’єктів з n позначається як Cnk, а функція ймовірності біномного розподілу — ймовірність k успіхів у n випробуваннях
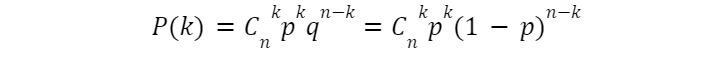
Яка ймовірність того, що станеться не більше, ніж k успіхів? Відповідь це питання дасть нам формулу функції розподілу. Очевидно, що для отримання не більше k успіхів треба отримати або 0 успіхів, або 1, або 2,…, k-1, k. Ці варіанти взаємозаперечні, тому ймовірність отримати не більше k успіхів дорівнюватиме сумі ймовірностей отримати 0 успіхів, 1,…, k. А кожну таку можливість ми знаємо. Тому функцією розподілу стане:
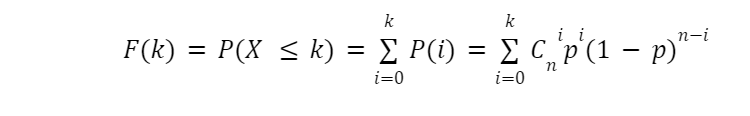
Нормальний розподіл
Існують випадкові величини, які є результатом впливу на них великої кількості дрібних незалежних випадкових чинників.
Такі значення, як зростання, вага, рівень кров’яного тиску, результат TOEFL, результат забігу на 100 метрів — це приклади таких величин. На ріст людини впливає понад 80 різних генів. На вагу, крім цього — спосіб життя, рівень спортивного навантаження, калорійність харчування.
Ці величини як би «обертаються» навколо середнього. Середній зріст людини знаходиться десь у діапазоні від 160 до 180 см. Дорослі люди вище або нижче трапляються рідше за інших. До того ж ймовірність зустріти як дуже високу людину, так і дуже низьку, приблизно однакова.
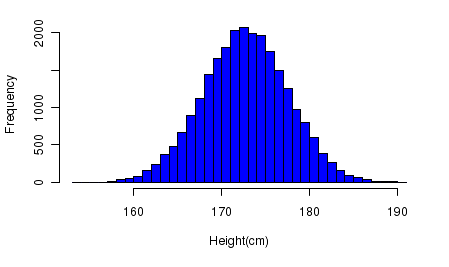
Джерело: Countbio
Подивимося на гістограму частот росту набору понад 25 тис. 18-річних людей, отриману на основі даних статистичного агентства SOCR. Ми побачимо, що найбільша зустрічальність відповідає середньому зростанню приблизно 172 сантиметри. Сам розподіл загалом симетричний.
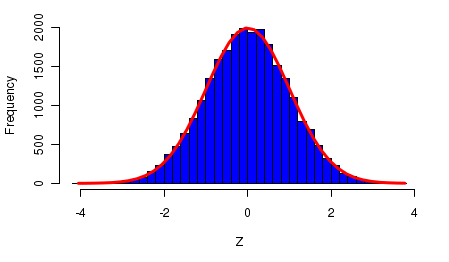
Джерело: Countbio
Такий графік може бути наближений до кривої, нагадувати дзвін за формою:
Якщо збільшувати розмір вибірки, графік гістограми буде все більше схожий на дзвоноподібну криву. Це властивість усіх випадкових величин, що є середнім рядом незалежних випадкових факторів (як у разі росту або ваги).
Подібний дзвоноподібний розподіл називається нормальним розподілом.
Цей розподіл визначається двома параметрами — середнім та дисперсією. Більшість значень такого розподілу розташовано навколо його середнього. Сильні відхилення від середнього в більшу чи меншу сторону малоймовірні. Чим далі відхилення від середнього значення, тим менша ймовірність такої події.
Нормальний розподіл зі значеннями середнього та дисперсії 0 та 1 називається стандартним нормальним розподілом. Його формула щільності була отримана як результат якогось граничного процесу і являє собою:
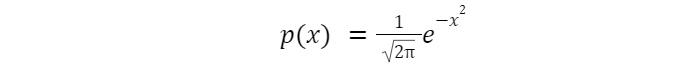
Функцією розподілу буде функція площі під графіком такої кривої (певний інтеграл зі змінною верхньою межею від функції вище). Для її підрахунку можна використовувати спеціальні таблиці або програми.



