Что такое распределения
Как устроены случайности.
Число, выпавшее на игральном кубике, возраст прохожего, время ожидания самолета — все это случайные величины. В работе мы тоже сталкиваемся с ними. Сколько людей сегодня зайдет на сайт, какой доход получит компания в этом месяце, не может быть известно заранее.
В теории вероятностей случайная величина — это переменная, которая может принимать набор возможных значений в зависимости от случая.
Распределение вероятностей — это закон, описывающий значения случайной величины и вероятности их появления.
В реальности случайные величины часто сложно устроены. Но в математике удалось найти закономерности их поведения. Рассказываем об основных.
Равномерное распределение
Классический пример — подбрасывание монетки. Это случайная величина с двумя исходами — орел или решка. Будем считать, что вероятность получить орла или решку одинакова и равна 1/2.
Теперь рассмотрим шестигранный игральный кубик. Выпавшее на нем число — это случайная величина, принимающая значения от 1 до 6, каждое с вероятностью 1/6.
Подобный закон сработает и если мы выберем произвольную цифру, например, в лотерейном билете. Мы приходим к случайной величине, принимающей десять различных значений (от 0 до 9 с шагом 1), каждое с вероятностью 1/10.
В общем случае возьмем произвольное число исходов. Мы приходим к случайной величине, принимающей n значений {1,2,3, ..., n}, каждое с вероятностью 1/n. Такое распределение называется дискретным равномерным распределением. Его функция вероятности вне зависимости от конкретного значения будет равна:
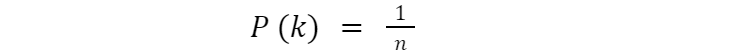
График такой функции вероятностей на некотором отрезке [a, b] будет выглядеть так:
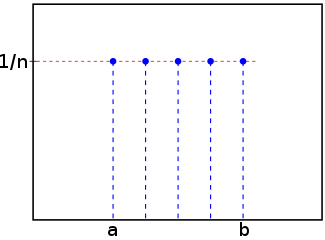
Источник: Wikipedia
Помимо функции вероятности, со случайной величиной связывают еще один объект. Чтобы узнать, с какой вероятностью значение случайной величины будет меньше или больше какого-то числа, используется функция распределения. Это вероятность, что случайная величина будет меньше или равна произвольному значению, P(Xk). Вероятность среди объектов {1, ..., n} получить значение, меньше или равное k, будет равна k/n. Так, мы получаем функцию распределения F(k)=k/n.
Вот ее график:
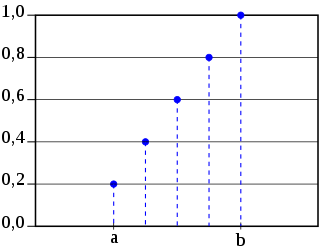
Источник: Wikipedia
В дискретной модели число возможных значений случайной величины конечно. Рассмотрим задачу с непрерывным распределением. Человек попадает на железнодорожную платформу равновероятно в случайный момент времени. На эту платформу каждые 30 минут приходит поезд. Следует понять, какова вероятность ожидания поезда более 20 минут.
Такая задача приводит нас к понятию непрерывного равномерного распределения. Здесь ожидание поезда — случайная величина, которая будет принимать значения на отрезке от 0 до 30. Вероятность получить любое численное значение на промежутке от 0 до 30 — постоянна. Таким образом, плотность распределения будет представлять собой константу. Эта константа должна быть такой, чтобы площадь под графиком плотности равнялась единице.
В нашем случае плотность вероятности будет равна 1/30. В общем случае — 1/(b-a).
График:
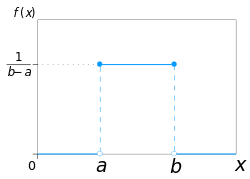
Источник: Wikipedia
Функция распределения F(x) — это вероятность ожидания поезда от a до x минут. Она находится как площадь под графиком от а до x функции плотности f. Это будет F(x)=x/30, а в общем случае F(x)=(x-a)/(b-a).
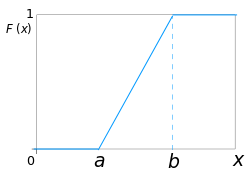
Источник: Wikipedia
Как видно, функция распределения — это интеграл от плотности распределения.
Чтобы решить нашу задачу, нужно подсчитать значение P(x>20). Его можно найти как площадь прямоугольника с шириной 10 (от 20 до 30) и высотой 1/30. Его также можно вычислить как значение 1-F(20). И в том, и в другом случае ответ будет ⅓. Вероятность прождать больше 20 минут составит ⅓.
Все значения равномерного распределения в заданном диапазоне равновероятны.
Распределение Бернулли
Говорить о равномерном распределении мы начали с классического эксперимента с монеткой. Там вероятность обоих исходов была одинаковой. А если рассмотреть монету, которая будет падать орлом c вероятностью p, и решкой — с вероятностью q?
Пусть случайная величина с 2 исходами принимает значение 1 с вероятностью p, и значение 0 c вероятностью q, так что p+q=1.
Такое распределение применимо и в жизни. Если вы хорошо подготовились, то вероятность сдать экзамен больше, чем завалить. Опытный стрелок с большей вероятностью попадет в мишень, чем промахнется.
Вот функция вероятностей такого распределения:
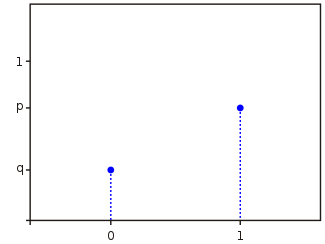
Источник: Wikipedia
У самой случайной величины 2 значения — 0 и 1. Однако ее функция распределения определяется для всех действительных чисел:
Значение меньше нуля у случайной величины не получится никогда — она принимает только 0 и 1. F(x)=0 для всех x<0.
Значение 0 будет с вероятностью q по определению. F(0)=q.
Найдем F(x)=P(X<x) для 0<x<1. Значения 0<x<1 случайная величина не принимает. Единственное ее значение, которое меньше таких x — это 0. Значит, вероятность P(X<x) для 0<x<1 — это P(X=0). Тогда F(x) для любого 0<x<1 — это F(0) : F(x)=F(0)=q.
Найдем вероятность получить значение, меньше или равное 1. Так как случайная величина принимает всего 2 значения и оба из них <=1, то эта вероятность будет равна 1: P(X<=1)=P(X=0 или X=1)=1.
То же касается и любого x>1 : P(x)=P(1)=1.
График F(x):
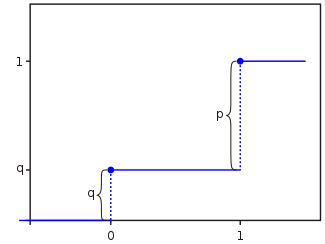
Источник: Wikipedia
Биномиальное распределение
Случается, что рассматривается не одно испытание, а несколько подряд.
Случается, что рассматривается не одно испытание, а несколько подряд.
Например, коллегия врачей решает, болен ли пациент. Два врача считают, что да, а один — что нет.
Модель телефона может содержать различные дефекты. При осмотре выяснилось, что у одного телефона дефекты содержат дисплей и аккумулятор, а у другого — только аккумулятор.
Оценим вероятности таких событий. Предположим, что вероятность события одинакова внутри серии. Так, допустим, что с одинаковой вероятностью p каждый из врачей примет положительное решение. Вероятность дефектов в новом телефоне одинакова.
В этих примерах проводится серия экспериментов Бернулли: есть n экспериментов, в каждом из которых вероятность успеха равна p, вероятность неудачи — q. Как оценить вероятность, что в n испытаниях будет ровно k успехов?
Рассмотрим случай из 3 испытаний и найдем вероятность получить 2 успеха из 3. Если p — вероятность успеха, а q — вероятность неудачи, то вероятности различных комбинаций в этих экспериментах будут такими:
Вероятность 3 успехов в 3 испытаниях =ppp=p3
Вероятность успехов в 1-м и 2-м испытании и неудачи в 3-м = ppq=p2q
Вероятность успехов в 1-м и 3-м испытании и неудачи во 2-м = pqp=p2q
Вероятность успехов в 1-м испытании и неудач во 2-м и 3-м = pqq=q2p
Вероятность неудачи в 1-м испытании и успехов во 2-м и 3-м = qpp=p2q
Вероятность неудачи в 1-м и 3-м испытании и успеха во 2-м = qpq=q2p
Вероятность неудачи в 1-м и 2-м испытании и успеха в 3-м = qqp=q2p
Вероятность 3 неудач в 3 испытаниях =qqq=q3
Нас интересуют случаи 2 успехов и 1 неудачи. Таких случаев 3, и вероятность каждого p2q. Они отличаются лишь тем, в каких конкретно из 3 экспериментов произошло 2 успеха, а в каком — неудача.
Таким образом, вероятность 2 успехов из 3 представляет собой 3p2q.
То, что коэффициент равен трем, — неслучайно. Это количество вариантов получить ровно 2 успеха в 3 экспериментах, то есть выбрать 2 места из 3 возможных. Число способов выбрать 2 объекта из 3 — это число сочетаний C23 =3
В общем случае число способов выбрать k объектов из n обозначается как Cnk, а функция вероятности биномиального распределения — вероятность k успехов в n испытаниях — будет
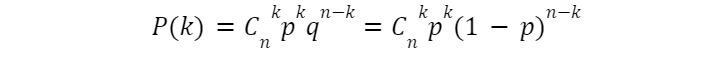
Какова вероятность того, что произойдет не более k успехов? Ответ на этот вопрос даст нам формулу функции распределения. Явно, что для получения не более k успехов надо получить либо 0 успехов, либо 1, либо 2, …, k-1, k. Эти варианты взаимоисключающие, потому вероятность не более k успехов будет равна сумме вероятностей получить 0 успехов, 1,..., k. А каждую такую вероятность мы знаем. Потому функцией распределения станет:
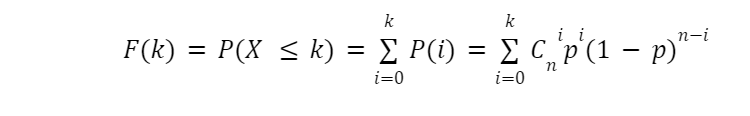
Нормальное распределение
Существуют случайные величины, которые представляют собой результат влияния на них большого числа маленьких независимых случайных факторов.
Такие значения, как рост, вес, уровень кровяного давления, результат TOEFL, результат забега на 100 метров, — это примеры таких величин. На рост человека влияет более 80 различных генов. На вес, кроме этого, — образ жизни, уровень спортивной нагрузки, калорийность питания.
Эти величины как бы «вращаются» вокруг среднего. Средний рост человека находится где-то в диапазоне от 160 до 180 см. Взрослые люди выше или ниже встречаются реже остальных. К тому же вероятность встретить как очень высокого человека, так и очень низкого, примерно одинакова.
Источник: Countbio
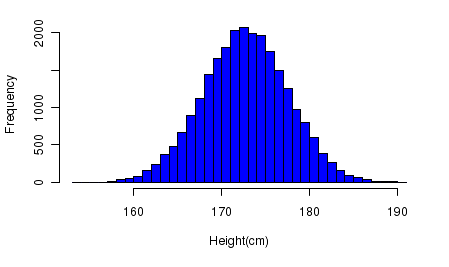
Посмотрим на гистограмму частот роста набора свыше 25 тыс. 18-летних людей, полученную на основе данных статистического агентства SOCR. Мы увидим, что наибольшая встречаемость соответствует среднему росту примерно в 172 сантиметра. Само распределение в общем симметрично.
Источник: Countbio
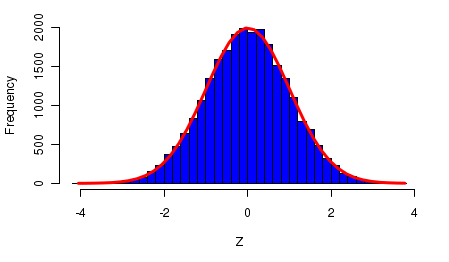
Такой график может быть приближен к кривой, по форме напоминающей колокол:
Если увеличивать размер выборки, график гистограммы будет все более похож на колоколообразную кривую. Это свойство всех случайных величин, представляющих собой среднее ряда независимых случайных факторов (как в случае роста или веса).
Подобное колоколообразное распределение называется нормальным распределением.
Это распределение определяется двумя параметрами — средним и дисперсией. Большинство значений у такого распределения расположено вокруг его среднего. Сильные отклонения от среднего в большую или меньшую сторону — маловероятны. Чем дальше отклонение от среднего значения, тем меньше вероятность такого события.
Нормальное распределение со значениями среднего и дисперсии 0 и 1 называется стандартным нормальным распределением. Его формула плотности была получена как результат некоего предельного процесса и представляет собой:
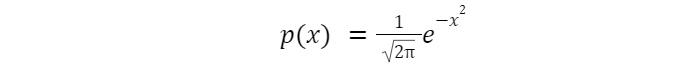
Функцией распределения будет функция площади под графиком такой кривой (определенный интеграл с переменным верхним пределом от функции выше). Для ее подсчета можно использовать специальные таблицы или приложения.







