Повний гайд з алгоритмів сортування на Java для новачків ч. 2
Частина 2. Сортуємо методом Шелла, підрахунком і швидким способом
У цій статті продовжуємо ознайомлюватися з алгоритмами сортування на Java. Що це таке, навіщо вони потрібні та як сортувати вставкою, вибором, бульбашкою й не тільки, розібрали тут, а в цьому матеріалі розглядаємо, як працює швидке сортування, сортування Шелла та сортування підрахунком.
Ефективність алгоритмів сортування
Як ми писали у першій частині статті, ефективність алгоритму визначає його часова складність — інакше кажучи, наскільки довго він виконуватиметься, залежно від кількості вхідних даних. Також зазначимо часову складність алгоритмів, які розбиратимемо на прикладах нижче:
O(n log n), де n — кількість вхідних даних:
- швидке сортування Java;
- сортування Шелла на Java.
O(n + K), де n — кількість елементів у вхідному масиві, а K — діапазон вхідних даних:
- сортування підрахунком Java.
Швидке сортування Java
Швидке сортування — це алгоритм сортування, що ґрунтується на стратегії «розділяй і володарюй».
Один елемент обирають як опорний, а потім елементи, що менші за нього, переміщують вліво, а ті, що більші, — вправо. Потім та сама процедура рекурсивно виконується у кожній частині.
Алгоритм швидкого сортування Java
Основний процес у швидкому сортуванні — розбиття (partition). Він поміщає опорний елемент (pivot) у відповідну позицію у відсортованому масиві, переміщуючи всі елементи, які менші за нього, ліворуч, а які більші за нього — праворуч.
Функція partition() викликається рекурсивно з кожного боку від опорного елемента після того, як його розташовано в належній позиції. У результаті отримуємо відсортований масив.
Є кілька варіантів вибору опорного елемента:
- завжди вибирати перший елемент;
- завжди вибирати останній елемент (реалізовано нижче);
- вибирати випадковий елемент;
- вибирати середній елемент.
Логіка проста: починаємо з крайнього лівого елемента та зберігаємо індекс меншого чи рівного елемента у змінній i. Якщо під час проходу знаходиться менший елемент, ми змінюємо місцями поточний елемент з елементом array[i]. А якщо ні, то ігноруємо поточний елемент.
Приклад: швидке сортування Java
Примітка. Як і в першій частині статті, усі методи сортування масиву в цій статті поміщені в пакет sorting і успадковують інтерфейс SortingMethod, який визначено в окремому класі. Код класу SortingMethod та класу, який демонструє результати роботи методів, можна знайти в кінці статті.
package sorting;
public class QuickSort implements SortingMethod {
// Swaps two elements
void swap(int[] array, int i, int j)
{
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
/* Takes last element as pivot,
moves the pivot element to the correct position,
and places all smaller to the left
all greater elements to the right
*/
int partition(int[] array, int left, int right)
{
// Choose the pivot element
int pivot = array[right];
// The correct position of the pivot found so far
int i = (left - 1);
for (int j = left; j <= right - 1; j++) {
// If current element is smaller than the pivot
if (array[j] < pivot) {
// Swap two elements
i++;
swap(array, i, j);
}
}
swap(array, i + 1, right);
return (i + 1);
}
// Partitions the array and sorts its parts
void quickSort(int[] array, int left, int right)
{
if (left < right) {
// Move the pivot to the correct position
int partitioningIndex = partition(array, left, right);
// Sort elements before
quickSort(array, left, partitioningIndex - 1);
// Sort elements after
quickSort(array, partitioningIndex + 1, right);
}
}
public void sort(int[] array){
quickSort(array, 0, array.length - 1);
}
}
Характеристики швидкого сортування
Часова складність у найкращому випадку: O (n log n), у середньому: O (n log n)
У найгіршому випадку: O(n2)
Додатковий простір: О(1). Але цей показник є актуальним, лише якщо не враховувати простір для стека рекурсії. Якщо ж його взяти до уваги, то сортування в найгіршому випадку виконає O(n) вкладених рекурсивних викликів і для нього буде потрібно O(n) додаткового простору.
Деякі переваги швидкого сортування:
- завдяки стратегії «розділяй і володарюй» цей метод спрощує розв'язання проблем;
- спосіб є ефективним для великих наборів даних;
- вимагає небагато пам'яті для роботи.
Недоліки швидкого сортування:
- У найгіршому випадку часова складність становить O(n2). Це відбувається, коли вибрано невдалий опорний елемент.
- Цей алгоритм є малоефективним для невеликих наборів даних.
- Це нестабільний метод сортування. Тобто, якщо маємо два елементи з одним і тим самим ключем, їхній порядок відносно один одного не буде дотримано. Так відбувається тому, що ми міняємо місцями елементи стосовно позиції опорного елемента й не враховуємо їхні початкові позиції.
Сортування підрахунком Java
Сортування підрахунком — це метод сортування, у якому підраховується кількість входжень кожного унікального елемента в масиві.
Дані про кількість зберігаються в окремому масиві, потім на основі цього окремого масиву обчислюється місце кожного елемента в цільовому масиві.
Сортування підрахунком є застосовним лише для тих випадків, коли діапазон можливих значень у вхідному масиві відомий заздалегідь.
Алгоритм сортування підрахунком Java
Для простоти розглянемо масив із сімома значеннями в діапазоні від 0 до 5. Вхідний масив: [1, 4, 1, 2, 3, 5, 2]
Знайдемо максимальне значення у вихідному масиві (max). У нашому випадку воно дорівнює 5.
Створимо допоміжний масив count довжиною max+1 для зберігання кількості входжень унікальних елементів та ініціалізуємо його нулями.
Кількість: 0, 0, 0, 0, 0, 0
(значення): 0, 1, 2, 3, 4, 5
Тепер збережемо в допоміжному масиві кількість входжень кожного унікального елемента. Якщо елемент повторюється, збільшуватимемо кількість його входжень.
Кількість: 0, 2, 2, 1, 1, 1
(значення): 0, 1, 2, 3, 4, 5
Тепер обчислимо й збережемо кумулятивну суму елементів у масиві count. Для цього здійснимо прохід по ньому, починаючи з другого елемента (з індексом 1), і додамо до кожного чергового значення попереднє.
Кількість: 0, 2, 4, 5, 6, 7
(значення): 0, 1, 2, 3, 4, 5
Створимо цільовий масив та ініціалізуємо його нулями.
Щоб алгоритм був стабільним, тобто щоб зберегти взаємне розташування елементів з однаковим значенням, здійснимо прохід по вхідному масиву у зворотному порядку. При цьому ми знайдемо індекс кожного елемента з вихідного масиву і розташуємо його в цільовому масиві.
Приклад: сортування підрахунком Java
package sorting;
// Java class implementing Counting Sort
class CountingSort implements SortingMethod {
public void sort(int array[]) {
int size = array.length;
int[] output = new int[size + 1];
// Find the maximum value in the array
int max = array[0];
for (int i = 1; i < size; i++) {
if (array[i] > max)
max = array[i];
}
// Create count array and fill it with zeros
int[] count = new int[max + 1];
for (int i = 0; i < max; ++i) {
count[i] = 0;
}
// Find and store the count of each element
for (int i = 0; i < size; i++) {
count[array[i]]++;
}
// Calculate and store cummulative sum of elements of count array
for (int i = 1; i <= max; i++) {
count[i] += count[i - 1];
}
// Traverse the initial array from the end and place the elements
// in output array into their respective positions
for (int i = size - 1; i >= 0; i--) {
output[count[array[i]] - 1] = array[i];
count[array[i]]--;
}
// Copy the sorted elements into the initial array
for (int i = 0; i < size; i++) {
array[i] = output[i];
}
}
}
Характеристики сортування підрахунком
Часова складність: O(n + K)
Додатковий простір: O(n + K)
Також сортування підрахунком має низку особливостей.
- У цьому методі використовують деякі припущення щодо даних. Наприклад, передбачено, що дані будуть у діапазоні від 0 до 5 або від 10 до 99 і так далі. Також передбачено, що вхідні дані будуть позитивними цілими числами. Проте цей алгоритм можна розширити, щоб застосовувати його і для обробки негативних чисел.
- Алгоритм не покладається на порівняння значень. Він хешує значення в допоміжному масиві та використовує їх для сортування.
- Метод використовує тимчасовий масив, отже, сортування проводиться не на місці.
- Сортування підрахунком є ефективним, якщо діапазон вхідних даних не набагато перевищує кількість елементів, які потрібно відсортувати. А якщо задано діапазон від 1 до 10 тис., а дані — 7, 5010, 258, 10 000 та 3 000, то він буде вкрай неефективним.
- Часто цей метод сортування використовують як підпрограму для інших алгоритмів, наприклад, для сортування за розрядами (radix sort).
Сортування підрахунком зазвичай працює швидше, ніж усі алгоритми, на основі порівняння (наприклад, сортування злиттям і швидке сортування), якщо діапазон вхідних значень має той самий порядок, що і їхня кількість. Цей метод є стабільним, і його легко програмувати. Але недоліки теж є:
- сортування підрахунком не є застосовним для дробових чисел, тому що вони не можуть бути індексами масиву;
- сортування підрахунком неефективне, коли діапазон значень набагато перевищує їхню кількість;
- сортування підрахунком не виконується на місці, а використовує додатковий простір для зберігання цільового масиву.
Сортування Шелла на Java
Сортування Шелла є варіантом сортування вставкою. Для сортування вставкою ми переміщуємо елементи лише на одну позицію вперед. Коли потрібно перемістити елемент далеко, виконується багато переміщень.
Суть сортування Шелла полягає в тому, щоб міняти місцями елементи, розташовані далеко один від одного. При використанні цього алгоритму ми робимо масив h-сортованим для великого значення h. Продовжуємо зменшувати значення h, поки воно не стане дорівнювати 1. Масив називається h-сортованим, якщо всі підмасиви кожного h-го елемента відсортовано.
Алгоритм сортування Шелла
- Ініціалізуємо значення розміру частини (h).
- Ділимо масив на менші частини з однаковою відстанню до h.
- Сортуємо ці частини за допомогою сортування вставкою.
- Повторюємо крок 1, доки список не буде відсортовано.
Приклад: сортування Шелла Java
package sorting;
class ShellSort implements SortingMethod {
public void sort(int array[])
{
int n = array.length;
// Start with a maximum gap, then reduce it
for (int gap = n/2; gap > 0; gap /= 2)
{
// Apply insertion sort to the current gap size.
for (int i = gap; i < n; i += 1)
{
int temp = array[i];
// shift earlier sorted elements until
// the correct position for a[i] is found
int j;
for (j = i; j >= gap && array[j - gap] > temp; j -= gap)
{
array[j] = array[j - gap];
}
// put the original a[i] stored in temp in its correct position
array[j] = temp;
}
}
}
}
Характеристики сортування Шелла
Часова складність наведеної вище реалізації сортування Шелла: O(n2). У цьому алгоритмі використовують вихідну послідовність Шелла, у якій для кожної ітерації інтервал зменшується наполовину. Існує багато інших способів зменшення інтервалу, які дозволяють підвищити продуктивність алгоритму.
Складність сортування Шелла в гіршому випадку становить O(n2). Якщо вихідний масив уже відсортовано, то загальна кількість порівнянь дорівнює розміру масиву. Тому складність у найкращому випадку: O(n log n). Складність сортування Шелла в середньому випадку: O(n log n).
Незалежно від послідовності інтервалів, просторова складність сортування Шелла становить О(1).
Код для демонстрації часу сортування
Створіть папку sorting і перемістіть туди файли з кодом усіх класів, що ми розглянули вище (наприклад, код класу ShellSort — у файл ShellSort.java і так далі).
Створіть у тій самій папці файл SortingMethod.java з таким кодом:
package sorting;
// Java class declaring SortingMethod interface
interface SortingMethod {
// Sorts an array
public void sort(int array[]);
}
У тій самій папці створіть файл SortingDemo.java з таким кодом:
package sorting;
// Java class demonstrating different sorting methods
public class SortingDemo {
// Prints an array
static void printArray(int array[])
{
int n = array.length;
for (int i = 0; i < n; ++i)
System.out.print(array[i] + " ");
System.out.println();
}
// Main method
public static void main(String args[])
{
System.out.println();
System.out.println("* Array sorting demo *");
System.out.println();
// Declare the array of sorting method instances
SortingMethod sortingMethods[] = {
new QuickSort(),
new CountingSort(),
new ShellSort()
};
// Demonstrate that methods work
for (int i = 0; i < sortingMethods.length; i++){
System.out.println(sortingMethods[i].getClass().toString());
// Declare the initial array
int array[] = { 9, 8, 10, 3, 4 };
// Show initial array
System.out.print("Initial array: ");
printArray(array);
// Store startTime
double startTime = System.nanoTime();
// Sort the array and show its new state
sortingMethods[i].sort(array);
// Measure method execution time
double endTime = System.nanoTime();
double duration = (endTime - startTime) / 1000000;
System.out.print("Resulting array: ");
printArray(array);
System.out.println("Execution time, ms: " + duration);
System.out.println();
}
}
}
Для компіляції відкрийте командний рядок і перейдіть до каталогу, де розташована папка sorting (в її батьківський каталог).
Для компіляції всіх файлів виконайте команду:
javac sorting/*.java
І, нарешті, запустіть демо:
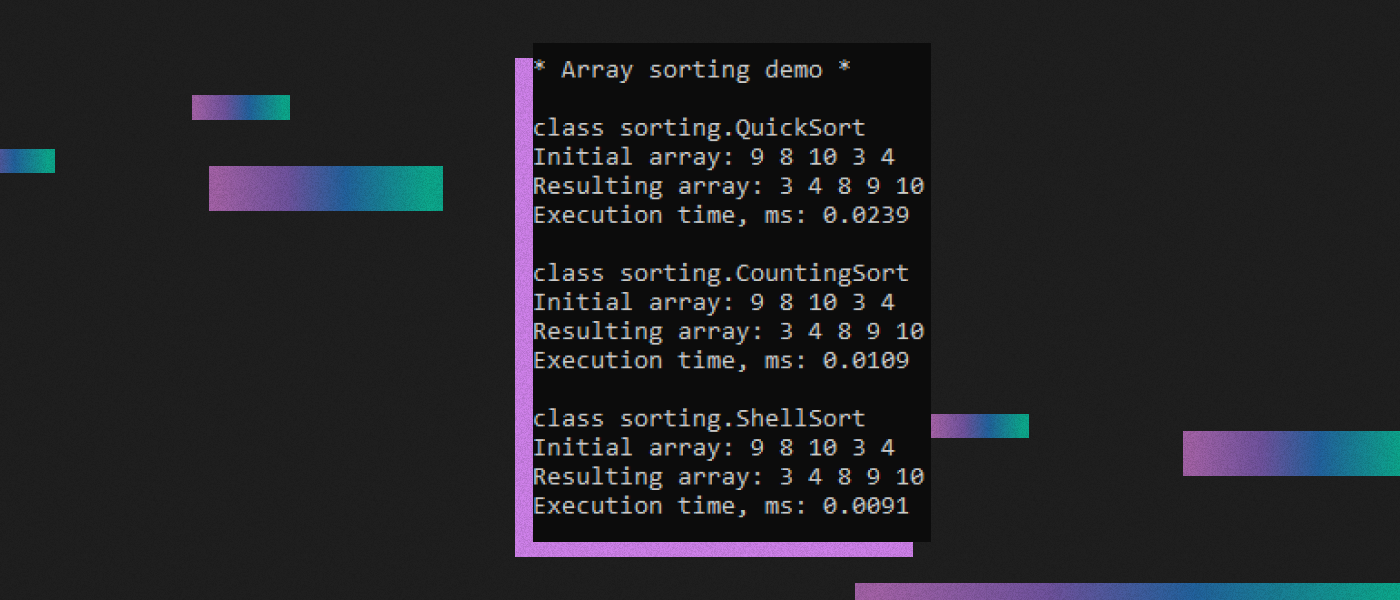
java sorting.SortingDemo
Результат: