Полный гайд по алгоритмам сортировки на Java для новичков ч. 2
Часть 2. Сортируем методом Шелла, подсчетом и быстрым способом
В этой статье продолжаем знакомиться с алгоритмами сортировки на Java. Что это такое, зачем они нужны и как сортировать вставкой, выбором, пузырьком и не только, разобрали здесь, а в этом материале смотрим, как работает быстрая сортировка, сортировка Шелла и сортировка подсчетом.
Эффективность алгоритмов сортировки
Как мы писали в первой части статьи, эффективность алгоритма определяет его временная сложность — иначе говоря, насколько долго он будет выполняться, в зависимости от количества входных данных. Также напомним временную сложность алгоритмов, которые будем разбирать на примерах ниже:
O(n log n), где n — количество входных данных:
- быстрая сортировка Java;
- сортировка Шелла на Java.
O(n + K), где n — количество элементов во входном массиве, а K — диапазон входных данных:
- сортировка подсчетом Java.
Быстрая сортировка Java
Быстрая сортировка — это алгоритм сортировки, основанный на стратегии «разделяй и властвуй».
Один элемент выбирается в качестве опорного, а затем элементы, которые меньше него, перемещаются влево, а те, которые больше, — вправо. Затем та же процедура рекурсивно выполняется в каждой части.
Алгоритм быстрой сортировки Java
Основной процесс в быстрой сортировке — разбиение (partition). Он помещает опорный элемент (pivot) в соответствующую позицию в отсортированном массиве, перемещая все элементы, которые меньше него, влево, а которые больше него — вправо.
Функция partition() вызывается рекурсивно с каждой стороны от опорного элемента после того, как он помещается в надлежащее положение. В результате получаем отсортированный массив.
Есть несколько вариантов выбора опорного элемента:
- всегда выбирать первый элемент;
- всегда выбирать последний элемент (реализован ниже);
- выбирать случайный элемент;
- выбирать средний элемент.
Логика проста: начинаем с крайнего левого элемента и храним индекс меньшего или равного элемента в переменной i. Если при проходе находится меньший элемент, мы меняем местами текущий элемент с элементом array[i]. В противном случае — игнорируем текущий элемент.
Пример: быстрая сортировка Java
Примечание. Как и в первой части статьи, все методы сортировки массива в этой статье помещены в пакет sorting и наследуют интерфейс SortingMethod, который определен в отдельном классе. Код класса SortingMethod и класса, который демонстрирует результаты работы методов, можно посмотреть в конце статьи.
package sorting;
public class QuickSort implements SortingMethod {
// Swaps two elements
void swap(int[] array, int i, int j)
{
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
/* Takes last element as pivot,
moves the pivot element to the correct position,
and places all smaller to the left
all greater elements to the right
*/
int partition(int[] array, int left, int right)
{
// Choose the pivot element
int pivot = array[right];
// The correct position of the pivot found so far
int i = (left - 1);
for (int j = left; j <= right - 1; j++) {
// If current element is smaller than the pivot
if (array[j] < pivot) {
// Swap two elements
i++;
swap(array, i, j);
}
}
swap(array, i + 1, right);
return (i + 1);
}
// Partitions the array and sorts its parts
void quickSort(int[] array, int left, int right)
{
if (left < right) {
// Move the pivot to the correct position
int partitioningIndex = partition(array, left, right);
// Sort elements before
quickSort(array, left, partitioningIndex - 1);
// Sort elements after
quickSort(array, partitioningIndex + 1, right);
}
}
public void sort(int[] array){
quickSort(array, 0, array.length - 1);
}
}
Характеристики быстрой сортировки
Временная сложность в наилучшем случае: O (n log n), в среднем: O (n log n)
В наихудшем случае: O(n2)
Дополнительное пространство: O(1). Но этот показатель актуален только если не учитывать пространство для стека рекурсии. Если же учитывать, то в наихудшем случае сортировка выполнит O(n) вложенных рекурсивных вызовов и для нее потребуется O(n) дополнительного места.
Среди преимуществ быстрой сортировки:
- благодаря стратегии «разделяй и властвуй» этот метод упрощает решение проблем;
- способ эффективен для больших наборов данных;
- требует немного памяти для работы.
Недостатки быстрой сортировки:
- В худшем случае временная сложность составляет O(n2). Это происходит, когда выбран неудачный опорный элемент.
- Этот алгоритм малоэффективен для небольших наборов данных.
- Это нестабильный метод сортировки. То есть, если есть два элемента с одним и тем же ключом, их порядок относительно друг друга не будет соблюден. Так происходит потому, что мы меняем местами элементы относительно позиции опорного элемента и не учитываем их исходные позиции.
Сортировка подсчетом Java
Сортировка подсчетом — это метод сортировки, при котором подсчитывается количество вхождений каждого уникального элемента в массиве.
Данные о количестве сохраняются в отдельном массиве, затем на основании этого отдельного массива вычисляется место каждого элемента в целевом массиве.
Сортировка подсчетом подходит лишь для тех случаев, когда заранее известен диапазон возможных значений во входном массиве.
Алгоритм сортировки подсчетом Java
Для простоты рассмотрим массив с семью значениями в диапазоне от 0 до 5. Входной массив: [1, 4, 1, 2, 3, 5, 2]
Найдем максимальное значение в исходном массиве (max). В нашем случае оно равно 5.
Создадим вспомогательный массив count длиной max+1 для хранения количества вхождений уникальных элементов и инициализируем его нулями.
Количество: 0, 0, 0, 0, 0, 0
(значения): 0, 1, 2, 3, 4, 5
Теперь сохраним во вспомогательном массиве количество вхождений каждого уникального элемента. Если какой-либо элемент повторяется, увеличиваем количество его вхождений..
Количество: 0, 2, 2, 1, 1, 1
(значения): 0, 1, 2, 3, 4, 5
Теперь вычислим и сохраним кумулятивную сумму элементов в массиве count. Для этого совершим проход по нему, начиная со второго элемента (с индексом 1), и прибавим к каждому очередному значению предыдущее.
Количество: 0, 2, 4, 5, 6, 7
(значения): 0, 1, 2, 3, 4, 5
Создадим целевой массив и инициализируем его нулями.
Чтобы алгоритм был стабильным, то есть чтобы сохранить взаимное расположение элементов с одинаковым значением, совершим проход по входному массиву в обратном порядке. При этом мы будем находить индекс каждого элемента из исходного массива и помещать его в целевой массив.
Пример: сортировка подсчетом Java
package sorting;
// Java class implementing Counting Sort
class CountingSort implements SortingMethod {
public void sort(int array[]) {
int size = array.length;
int[] output = new int[size + 1];
// Find the maximum value in the array
int max = array[0];
for (int i = 1; i < size; i++) {
if (array[i] > max)
max = array[i];
}
// Create count array and fill it with zeros
int[] count = new int[max + 1];
for (int i = 0; i < max; ++i) {
count[i] = 0;
}
// Find and store the count of each element
for (int i = 0; i < size; i++) {
count[array[i]]++;
}
// Calculate and store cummulative sum of elements of count array
for (int i = 1; i <= max; i++) {
count[i] += count[i - 1];
}
// Traverse the initial array from the end and place the elements
// in output array into their respective positions
for (int i = size - 1; i >= 0; i--) {
output[count[array[i]] - 1] = array[i];
count[array[i]]--;
}
// Copy the sorted elements into the initial array
for (int i = 0; i < size; i++) {
array[i] = output[i];
}
}
}
Характеристики сортировки подсчетом
Временная сложность: O(n + K)
Дополнительное пространство: O(n + K)
Также у сортировки подсчетом есть ряд особенностей:
- В этом методе используются некоторые допущения насчет данных. Например, предполагается, что данные будут находиться в диапазоне от 0 до 5 или от 10 до 99 и так далее. Также предполагается, что входные данные будут положительными целыми числами. При этом алгоритм можно расширить для обработки отрицательных чисел.
- Алгоритм основан не на сравнении значений. Он хэширует значения во вспомогательном массиве и использует их для сортировки.
- Метод использует временный массив, потому сортировка производится не на месте.
- Сортировка подсчетом эффективна, если диапазон входных данных ненамного превышает количество элементов, которые требуется отсортировать. А если задан диапазон от 1 до 10 тыс., а данные — 7, 5010, 258, 10 000 и 3 000, то он будет крайне неэффективным.
- Часто этот метод сортировки используется как подпрограмма для других алгоритмов, например, для сортировки по разрядам (radix sort).
Сортировка подсчетом обычно работает быстрее, чем все алгоритмы, основанные на сравнении (например, сортировка слиянием и быстрая сортировка), если диапазон входных значений того же порядка, что и их количество. Этот метод стабильный и его легко программировать. Но недостатки тоже есть:
- сортировка подсчетом не подходит для дробных чисел, потому что они не могут быть индексами массива;
- сортировка подсчетом неэффективна, когда диапазон значений намного превышает их количество;
- сортировка подсчетом не выполняется на месте, а использует дополнительное пространство для хранения целевого массива.
Сортировка Шелла на Java
Сортировка Шелла — это вариант сортировки вставкой. При сортировке вставкой мы перемещаем элементы только на одну позицию вперед. Когда необходимо переместить элемент далеко, выполняется много перемещений.
Суть сортировки Шелла состоит в том, чтобы менять местами элементы, расположенные далеко друг от друга. При использовании этого алгоритма мы делаем массив h-сортированным для большого значения h. Продолжаем уменьшать значение h, пока оно не станет равным 1. Массив называется h-сортированным, если все подмассивы каждого h-го элемента отсортированы.
Алгоритм сортировки Шелла
- Инициализируем значение размера части (h).
- Делим массив на меньшие части с одинаковым расстоянием до h.
- Сортируем эти части с помощью сортировки вставкой.
- Повторяем шаг 1, пока список не будет отсортирован.
Пример: сортировка Шелла Java
package sorting;
class ShellSort implements SortingMethod {
public void sort(int array[])
{
int n = array.length;
// Start with a maximum gap, then reduce it
for (int gap = n/2; gap > 0; gap /= 2)
{
// Apply insertion sort to the current gap size.
for (int i = gap; i < n; i += 1)
{
int temp = array[i];
// shift earlier sorted elements until
// the correct position for a[i] is found
int j;
for (j = i; j >= gap && array[j - gap] > temp; j -= gap)
{
array[j] = array[j - gap];
}
// put the original a[i] stored in temp in its correct position
array[j] = temp;
}
}
}
}
Характеристики сортировки Шелла
Временная сложность приведенной выше реализации сортировки Шелла: O(n2). В этом алгоритме используется исходная последовательность Шелла, в которой на каждой итерации интервал уменьшается наполовину. Существует много других способов уменьшения интервала, которые позволяют повысить производительность алгоритма.
ССложность сортировки Шелла в худшем случае составляет O(n2). Если исходный массив уже отсортирован, то общее число сравнений равно размеру данного массива. Поэтому сложность в лучшем случае: O(n log n). Сложность сортировки Шелла в среднем случае: O(n log n).
Независимо от последовательности интервалов, пространственная сложность сортировки Шелла составляет О(1).
Код для демонстрации времени сортировки
Создайте папку sorting и переместите туда файлы с кодом всех рассмотренных выше классов (например, код класса ShellSort — в файл ShellSort.java и так далее).
Создайте в этой же папке файл SortingMethod.java с таким кодом:
package sorting;
// Java class declaring SortingMethod interface
interface SortingMethod {
// Sorts an array
public void sort(int array[]);
}
В той же папке создайте файл SortingDemo.java с таким кодом:
package sorting;
// Java class demonstrating different sorting methods
public class SortingDemo {
// Prints an array
static void printArray(int array[])
{
int n = array.length;
for (int i = 0; i < n; ++i)
System.out.print(array[i] + " ");
System.out.println();
}
// Main method
public static void main(String args[])
{
System.out.println();
System.out.println("* Array sorting demo *");
System.out.println();
// Declare the array of sorting method instances
SortingMethod sortingMethods[] = {
new QuickSort(),
new CountingSort(),
new ShellSort()
};
// Demonstrate that methods work
for (int i = 0; i < sortingMethods.length; i++){
System.out.println(sortingMethods[i].getClass().toString());
// Declare the initial array
int array[] = { 9, 8, 10, 3, 4 };
// Show initial array
System.out.print("Initial array: ");
printArray(array);
// Store startTime
double startTime = System.nanoTime();
// Sort the array and show its new state
sortingMethods[i].sort(array);
// Measure method execution time
double endTime = System.nanoTime();
double duration = (endTime - startTime) / 1000000;
System.out.print("Resulting array: ");
printArray(array);
System.out.println("Execution time, ms: " + duration);
System.out.println();
}
}
}
Для компиляции откройте командную строку и перейдите в каталог, в котором находится папка sorting (в ее родительский каталог).
Для компиляции всех файлов запустите команду:
javac sorting/*.java
И, наконец, запустите демо:
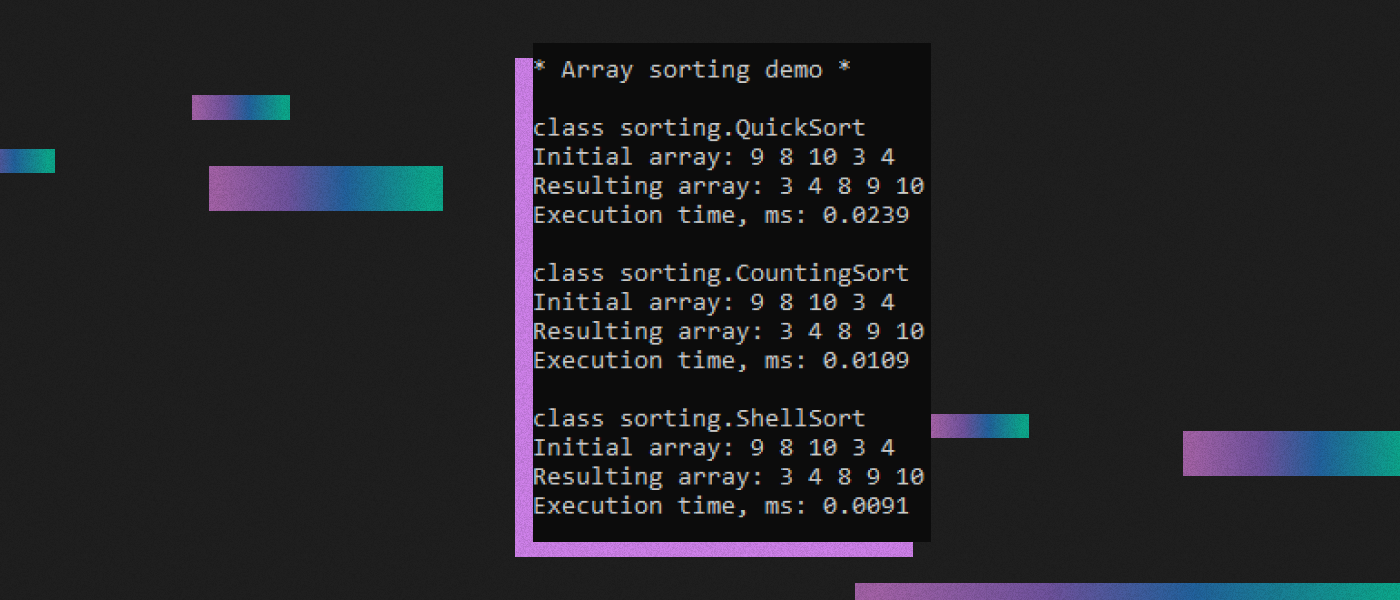
java sorting.SortingDemo
Результат: