Що таке лінійна регресія: повний гайд від robot_dreams

Сьогодні ми розглянемо роботу моделі машинного навчання в задачах із лінійною регресією: що для цього потрібно, як рахувати ефективність такої моделі та як модель взагалі функціонує.

Де застосовують лінійну регресію

Завдання простої лінійної регресії трапляються в машинному навчанні досить часто. Наприклад, коли потрібно вгадати деяке числове значення, скажімо, спрогнозувати кількість продажів товару в наступному році або вказати приблизну вартість житла за заданими параметрами-критеріями (близькості розташування до метро, за районом міста, розміром житлової площі тощо).

Формула лінійної регресії

У загальному вигляді лінійна модель має вигляд об'єкта x = (x₁, x₂, ..., x_d) з набором ознак із загальним числом d. Формула лінійної регресії:

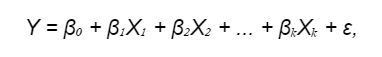
де:

• Y — це залежна змінна (відгук), яку ми намагаємося передбачити;
• β₀, β₁, β₂, ..., βₖ — це коефіцієнти регресії (ваги), які множаться на відповідні предиктори X_₁, X_₂, ..., X_ₖ. Ваги предикторів визначають, як кожен предиктор впливає на залежну змінну. Замість терміна «предиктор» можуть використовувати інші поняття: «незалежна змінна», «фактор», «вхідні дані» тощо.
• ε — це розбіжність між передбаченими значеннями й фактичними, нормально розподілена випадкова величина (про помилки поговоримо трохи нижче).

У загальному вигляді лінійна модель має вигляд функції:

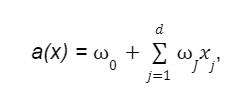
де:

• w0 — вільний коефіцієнт або зсув (він же bias);
• wJ — ваги або коефіцієнти.

Для зручності нотації лінійної моделі можна зробити припущення, що в нашій вибірці завжди наявна одинична константна ознака. Це дасть нам змогу вважати, що коефіцієнт при ній це і буде вільний w0. Таке припущення свідчить про те, що модель можна записувати просто як скалярний добуток а(x)= < w,х >, що зручно для аналізу.

Другий доданок можна розглядати як скалярний добуток вектора-стовпця ваг на вектор-стовпець ознак. При цьому варто мати на увазі, що ознаки мають бути речовинними й незалежними, вони мають впливати на результат лінійно.

Підготовка даних для моделі

Для лінійної моделі брати довільну вибірку нераціонально — результат, найімовірніше, буде посередній. Дані потрібно готувати, щоб модель працювала більш ефективно і точно.

Наприклад, якщо ми хочемо побудувати лінійну модель для передбачення ціни будинку, то наша вибірка має містити будинки з різних регіонів, з різною площею, кількістю кімнат тощо. Якщо ж ми візьмемо довільну вибірку, то вона може містити надто багато будинків з одного регіону або з однаковими характеристиками, що може призвести до того, що модель буде погано передбачати ціну будинків з інших регіонів або з іншими характеристиками.

Якщо дані містять шум або непотрібну інформацію, то модель може «плутатися» і давати неправильні прогнози. Тому на етапі попереднього опрацювання даних потрібно прибирати такі ознаки, залишаючи тільки найбільш важливі та інформативні.

Шкалювання

Предиктори можуть мати різні масштаби, що вплине на процес навчання та інтерпретацію коефіцієнтів. Якщо ваші предиктори мають різні масштаби, може знадобитися виконання шкалювання, щоб привести їх до одного масштабу. Для цього використовуйте стандартизацію або нормалізацію.

Коли необхідне шкалювання

Припустимо, у нас є набір даних про продажі автомобілів:

• Одна змінна — це ціна автомобіля. Може бути від кількох тисяч до кількох мільйонів доларів.
• Інша — кількість проданих машин. Може варіюватися від кількох штук до кількох тисяч штук.

Якщо ми не будемо масштабувати ці змінні, то модель лінійної регресії приділятиме більше уваги ціні автомобіля, ніж кількості проданих автомобілів. Це пов'язано з тим, що ціна автомобіля має ширший діапазон значень.

Що означає масштабувати в контексті лінійної регресії? Наприклад, ми можемо розділити ціну автомобіля на 1000, а кількість проданих автомобілів — на 100. Після масштабування обидві змінні матимуть діапазон значень від 0 до 1. Це зробить модель більш стійкою до шумів і аномалій, а також поліпшить її передбачувальну точність.

Приклад шкалювання

Ось приклад шкалювання ознак з використанням стандартизації (Z-перетворення) у Python за допомогою бібліотеки scikit-learn:

from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
# Генеруємо приклад даних (тут X — ознаки, y — цільова змінна)
X, y = ...
# Розділяємо дані на навчальний і тестовий набори
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# Створюємо об'єкт стандартизації
scaler = StandardScaler()
# Застосовуємо стандартизацію до навчальних даних і паралельно навчаємо шкалювальник
X_train_scaled = scaler.fit_transform(X_train)
# Застосовуємо ту саму стандартизацію до тестових даних (без повторного навчання)
X_test_scaled = scaler.transform(X_test)
# Створюємо і навчаємо модель лінійної регресії на відмасштабованих даних
model = LinearRegression()
model.fit(X_train_scaled, y_train)
# Оцінюємо продуктивність моделі
score = model.score(X_test_scaled, y_test)
# Отримуємо коефіцієнти регресії
coefficients = model.coef_
intercept = model.intercept_
print("Продуктивність моделі (R-squared):", score)
print("Коефіцієнти регресії:", coefficients)
print("Вільний член:", intercept)

Цей метод перетворює кожну ознаку так, щоб вона мала середнє значення 0 і стандартне відхилення 1. Потім ми навчаємо модель лінійної регресії на відмасштабованих даних і оцінюємо продуктивність моделі.

Бінаризація даних

Один із популярних методів підготовки інформації — бінаризація даних, тобто процес перетворення кількісних ознак на бінарні (двійкові) ознаки на основі певного порогового значення. У результаті бінаризації ознак кожне значення або стає 0, якщо воно менше за порогове значення, або 1, якщо воно більше або дорівнює порогу.

Приклад бінаризації в Python з використанням бібліотеки NumPy

Бібліотека встановлюється командою pip install numpy.

Припустимо, ми маємо справу з кількісною ознакою AGE («Вік»), і ви хочете перетворити його на бінарну ознаку «Старший 35 років». Зробити це можна так:

import numpy as np
# Створюємо масив із віком
ages = np.array([20, 25, 32, 35, 41, 46, 52, 53, 62])
# Задаємо поріг для бінаризації
threshold = 35
# Застосовуємо бінаризацію
binary_ages = (ages >= threshold).astype(int)
print(binary_ages)

Результат бінаризації:

[0 0 0 1 1 1 1 1 1]

У цьому прикладі 1 означає, що вік старший або дорівнює 35 років, а 0 — молодший 35 років.

Label Encoding

Label Encoding (Кодування міток) застосовують у задачах, коли потрібно представити категорії (наприклад, текстові або дискретні значення) у вигляді чисел, щоб їх можна було використовувати в алгоритмах машинного навчання. Кожній унікальній категорії присвоюють унікальне ціле число.

Приклад використання Label Encoding у задачі лінійної регресії

Припустимо, ми аналізуємо дані про продажі нерухомості, і у нас є категоріальна ознака «Клас житла» з категоріями, упорядкованими за ступенем розкоші: «Економ», «Стандарт», «Преміум». У цьому випадку можна використовувати Label Encoding для перетворення цієї ознаки на числовий формат, щоб лінійна регресія могла працювати з нею.

Приклад коду на Python з використанням бібліотеки scikit-learn:

from sklearn.preprocessing import LabelEncoder
from sklearn.linear_model import LinearRegression
# Створюємо набір даних з ознаками, включно з категоріальним "Клас житла"
data = {
    'Площа': [100, 150, 120, 80, 200],
    'Клас житла': ['Економ', 'Стандарт', 'Преміум', 'Економ', 'Преміум'],
    'Ціна': [200000, 300000, 350000, 150000, 450000]
}
# Ініціалізуємо LabelEncoder
label_encoder = LabelEncoder()
# Перетворюємо категоріальну ознаку "Клас житла" на числовий формат
data['Клас житла'] = label_encoder.fit_transform(data['Клас житла'])
# Поділяємо дані на ознаки та цільову змінну
X = data[['Площа', 'Клас житла']]
y = data['Ціна']
# Створюємо і навчаємо лінійну регресію
model = LinearRegression()
model.fit(X, y)
# Робимо прогноз
predicted_prices = model.predict(X)
print(predicted_prices)

One-Hot encoding

Для перетворення категоріальних змінних на числові можна застосовувати метод One-Hot encoding. Його алгоритм такий:

• Для кожної категоріальної змінної створюється вектор.
• Для кожного компонента вектора присвоюється значення 1, якщо значення категоріальної змінної відповідає цьому компоненту, і 0, якщо ні.
• Вектори об'єднуються в єдиний набір даних.

Приклад One-Hot encoding з використанням бібліотеки Python pandas

Приклад реалізації програмно:

import pandas as pd
# Створюємо датафрейм з категоріальними змінними
data = {'Колір': ['Червоний', 'Зелений', 'Синій', 'Червоний', 'Зелений']}
df = pd.DataFrame(data)
# Застосовуємо One-Hot encoding за допомогою функції get_dummies
one_hot_encoded = pd.get_dummies(df, columns=['Колір'])
print(one_hot_encoded)

Цей код демонструє застосування One-Hot encoding з використанням бібліотеки pandas. Ми створили DataFrame із категоріальною змінною «Колір», після чого використовували функцію pd.get_dummies() для виконання One-Hot encoding. Результат:

   Колір_Зелений  Колір_Червоний  Колір_Синій

0             0            1           0

1             1            0           0

2             0            0           1

3             0            1           0

4             1            0           0

Програмна реалізація моделі лінійної регресії

Для створення і навчання лінійної регресійної моделі важлива не тільки підготовка даних, а й визначення моделі за допомогою методу LinearRegression() — саме його ми викликали в прикладах вище. Розгляньмо його докладніше.

Припустимо, у нас є дані про площу будинків і їхню ціну, і ми хочемо побудувати модель для прогнозування цін на будинки на основі площі та кількості кімнат. У цьому прикладі ми використовуватимемо згенеровані дані для наочності.

Метод лінійної регресії має кілька параметрів, які можна налаштувати для визначення поведінки моделі. Ось деякі, що найчастіше використовують:

• fit_intercept (за замовчуванням=True) — цей параметр вказує, чи потрібно оцінювати перетин (intercept) моделі. Якщо він встановлений у True, то модель міститиме вільний член (перетин) у рівнянні лінійної регресії. Якщо встановлено в False, то модель проходитиме через початок координат.
• normalize (за замовчуванням=False) — цей параметр керує нормалізацією ознак перед навчанням моделі. Якщо встановлено в True, то ознаки будуть нормалізовані перед навчанням моделі. Нормалізація корисна, якщо ознаки мають різний масштаб.
• n_jobs (за замовчуванням=None) — цей параметр вказує кількість ядер CPU, які можна використовувати для навчання моделі. Якщо встановлено в None, то буде використовуватися одне ядро. Якщо ви вкажете позитивне число, то модель буде навчатися паралельно, що може прискорити процес на багатопроцесорних системах.
• positive (за замовчуванням=False) — цей параметр дає змогу налаштувати модель для виконання регресії з обмеженням на позитивні коефіцієнти.

import numpy as np
from sklearn.linear_model import LinearRegression
# Створюємо згенеровані дані (у реальності дані мають бути завантажені)
# Площа будинків у квадратних метрах
X_area = np.array([130, 150, 158, 175, 102, 144, 218, 228, 133, 158])
# Кількість кімнат у будинку
X_rooms = np.array([3, 2, 3, 4, 2, 3, 4, 5, 3, 3])
# Ціни на нерухомість
y = np.array([245000, 312000, 279000, 308000, 199000, 219000, 405000, 324000, 319000, 255000])
# Створюємо об'єкт моделі лінійної регресії
model = LinearRegression()
# Навчаємо модель на даних
# Об'єднуємо два предиктори в одну матрицю
X = np.column_stack((X_area, X_rooms))
model.fit(X, y)
# Тепер модель навчена і може робити передбачення
# Спрогнозуємо ціну для будинку площею 250 кв. метрів і 8 кімнатами
house_area = 250
house_rooms = 8
predicted_price = model.predict(np.array([[house_area, house_rooms]]))
print(f'Передбачена ціна для будинку площею {house_area} кв. метрів і {house_rooms} кімнатами: ${predicted_price[0]:.2f}')

Результат прогнозування

Способи завантаження даних

У реальності дані мають бути завантажені. Зазвичай їх експортують із зовнішніх джерел (баз даних, CSV-файлів, API, вебсервісів тощо). Вибір методу завантаження залежить від джерела даних і формату файлу з даними, з огляду на ваше конкретне завдання.

Розгляньмо кілька прикладів завантаження даних у Python:

Завантаження даних із CSV-файлу з використанням бібліотеки pandas:

import pandas as pd
# Завантаження даних із CSV-файлу
data = pd.read_csv('ім'я_файлу.csv')

Завантаження даних із зовнішніх джерел, як-от API:

import requests
import pandas as pd
# Запит даних із веб-API
response = requests.get('https://api.example.com/data')
data = pd.read_json(response.text)

Завантаження даних з Excel-файлу з використанням бібліотеки pandas:

import pandas as pd
# Завантаження даних з Excel-файлу
data = pd.read_excel('ім'я_файлу.xlsx')

Вимірювання помилки в задачах регресії

Для оцінювання продуктивності моделі та визначення того, наскільки точно модель передбачає числові значення (наприклад, цільову змінну) на нових даних, застосовують низку метрик.

Середньоквадратична помилка

Найпопулярнішою метрикою в задачах регресії є середньоквадратична помилка (Mean Squared Error, MSE). MSE вимірює середньоквадратичне відхилення між фактичними значеннями та передбачуваними значеннями моделі. Великі помилки роблять більший внесок у цю метрику.

Модифікованим варіантом цієї метрики є корінь із середньої квадратичної помилки (RMSE). Оскільки RMSE має ту саму розмірність, що й вихідні дані, вона краще інтерпретується.

RMSE

RMSE вимірює середнє абсолютне відхилення між фактичними значеннями та передбаченими значеннями моделі. Вона є популярною метрикою в задачах регресії та надає зрозуміле уявлення про те, наскільки точно модель пророкує значення цільової змінної. Що менше значення RMSE, то краще модель відповідає даним.

Ця метрика особливо актуальна, коли потрібно боротися із викидами. RMSE штрафує великі помилки (квадратично) сильніше, ніж маленькі, і таким чином робить модель більш чутливою до викидів.

Викиди в даних

Приклад викиду

Припустимо, що в нас є дані про зарплати (Y) і досвід роботи (X) для групи працівників:

• Досвід роботи (роки): 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15, 20
• Зарплата (тис. доларів): 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 150, 200

У цьому наборі даних значення зарплат 150 і 200 тисяч доларів є викидами, оскільки вони значно вищі за інші зарплати й не відповідають загальному тренду. Ці викиди можуть спотворити модель лінійної регресії та призвести до неправильних коефіцієнтів регресії та прогнозів.

Очевидно, що варто застосувати методи обробки даних:

• Видалити їх: просто прибрати викиди з набору даних, але це може втратити інформацію.
• Замінити на типові значення: замінити викиди на більш типові значення, щоб вони не спотворювали результати.
• Використовувати більш стійкі методи регресії: замість звичайної лінійної регресії можна використовувати методи, які менш чутливі до викидів, як-от робастна регресія або методи типу Хьюбера. Ці методи врахують викиди, але не дадуть їм занадто великої влади в моделі.

Висновок

Тепер ви маєте уявлення про один із найважливіших підходів до прогнозування в машинному навчанні та статистиці. Ми розповіли про головні принципи роботи лінійної регресії, підготовку даних для роботи моделі та деякі метрики для оцінювання ефективності роботи.

Лінійні моделі швидко навчаються і стійкі до шуму в даних, але в задачах з нелінійною залежністю вони слабкі та мало ефективні. Вони чутливі до викидів і за їх наявності можуть дуже помилятися в прогнозах.