Градієнтний спуск: алгоритм та приклад на Python

Градієнтний спуск — це один із методів оптимізації, який дозволяє нейронній мережі вчитися. Про те, як він працює і чому мережа починає «розуміти», що правильно, а що ні, читайте в цьому матеріалі.

Як навчають нейронки й навіщо потрібний градієнтний спуск

Ненавчена нейронна мережа — поганий помічник: вона поводиться непередбачувано і генерує випадкові відповіді. Але якщо підказати їй, що правильно, а що ні, вона зможе робити прогнози навіть точніше, ніж людина.

Але як саме цього досягти?

За замовчуванням сигнал у нейронці передається від вхідних рецепторів у перший і всі наступні приховані шари, доки не трансформується у сигнал для вихідного шару. Але поки параметри моделі — значення ваги та величина зміщення нейронів — не налаштовані, ми отримуватимемо деяку помилку. Щоб її мінімізувати, потрібно оптимізувати мережу.

Кінцева мета оптимізації — знайти такі значення параметрів, за яких функція помилки досягне свого мінімуму.

Один з основних методів оптимізації, які використовуються для досягнення цієї мети, — метод градієнтного спуску. Він допомагає знаходити напрямок, у якому функція помилки зменшується, та оновлювати параметри моделі відповідним чином.

Градієнтний спуск

Щоб зрозуміти суть методу, згадаємо математику.

Градієнт — це вектор, який спрямований у бік максимальної зміни функції.

У контексті нейронних мереж градієнт функції помилки допомагає визначити, як зміна того чи іншого параметра впливає на значення функції помилки. Іншими словами, він вказує, як потрібно змінити параметри моделі, щоб зробити помилку меншою.

Метод задіює вектор градієнта для визначення напрямку, у якому функція помилки зменшується найшвидше. Це дозволяє нам начебто «спускатися схилом помилки», наближаючись до мінімального значення функції. Параметри моделі оновлюються на кожній ітерації та рухаються у напрямку, протилежному градієнту функції помилки, поки ми не знайдемо точку у просторі параметрів, де помилка на навчальних даних буде мінімальною.

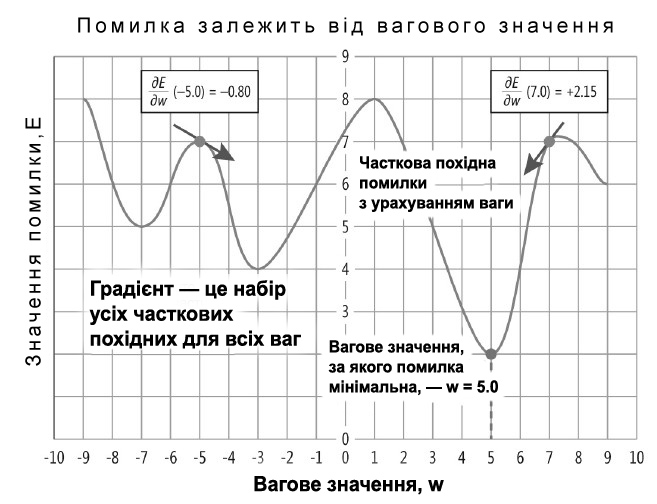
Починаючи з деяких початкових значень параметрів, ми обчислюємо градієнт функції помилки за цими параметрами. Потім змінюємо значення параметрів, віднімаючи деяку частку градієнта. Процес циклічно повторюється, поки значення параметрів не стануть оптимальними або поки функція помилки не перестане значно зменшуватися.

Алгоритм градієнтного спуску

Математично градієнтний спуск можна уявити так:

1. Ініціалізувати параметри моделі випадковими значеннями.

2. Подати вхідні дані в модель та отримати передбачення.

3. Обчислити значення функції помилки, порівнявши прогнози з фактичними значеннями. Як саме — залежить від конкретного завдання. Наприклад, у завданнях регресії можна використати формулу:

де n — кількість прикладів у навчальній вибірці, y — фактичне значення, Y — передбачуване значення цільової змінної.

4. Визначити градієнт функції помилки за кожним параметром моделі. Формула обирається залежно від обраної функції помилки.

5. Оновити значення параметрів за формулою:

нове значення параметра = старе значення параметра − learning rate * градієнт.

Learning rate (швидкість навчання) — це гіперпараметр, який контролює швидкість збіжності алгоритму градієнтного спуску та визначає розмір кроку, з яким оновлюються параметри моделі. Чим менший крок — тим більше часу знадобиться на навчання нейронної мережі та оновлення параметрів.

6. ППовторити кроки 2–5 для кожного етапу прогонки навчання (епохи) або до досягнення критерію зупинки.

Приклад корекції ваг нейронної мережі

Припустімо, у нас є повнозв'язна нейронна мережа прямого поширення. У неї є ваги зв'язку (вибрані випадково), і вони лежать у діапазоні значень [−0.5;0.5].

Повнозв'язна нейронна мережа прямого поширення

Верхній індекс означає приналежність до того чи іншого шару. У кожного нейрона є активаційна функція f(x). Кожне спостереження має свій відгук — d.

Проходячи цією мережею, ми отримуємо вектор спостережень:

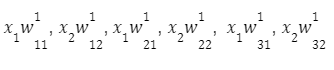
Для першого вузла першого шару отримуємо:

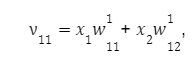
для другого:

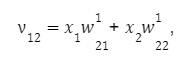
для третього:

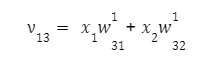
Проходячи через мережу, на виході нейрона ми матимемо деяке значення, отримане через функцію активації. Воно буде обчислено за формулою:

Пересуваючись далі мережею, ми отримуємо вектор спостережень:

Для кожного нейрона другого шару:

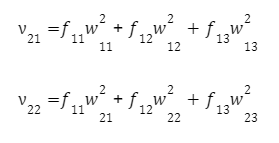
На першому нейроні другого шару:

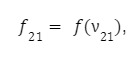
на другому:

Аналогічно доходимо до вихідного значення y. Оскільки ми знаємо бажане вихідне значення для нашого вектора x1 і x2 — d, нескладно підрахувати помилку на виході:

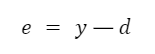
З цього моменту починається процес коригування ваги. Вона виконується у зворотному напрямку, з виходу на вхід. Відповідно до алгоритму backpropagation ми повинні обчислити локальний градієнт вихідного нейрона. Робиться це за формулою:

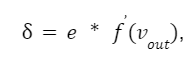
де f(v_out) — похідна функції активації вихідного нейрона.

Вихідною функцією активації може бути або гіперболічний тангенс, або сигмоїда.

Читайте також Повний гайд за функціями активації нейронних мереж

Ці функції відрізняються лише рівнем (для гіперболічного тангенсу це діапазон від −1 до 1, а для логістичної функції — проміжок від −0.5 до 0,5).

Припустімо, ми обрали функцію:

Її похідна виглядатиме як:

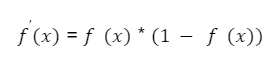
А локальний градієнт можна визначити як:

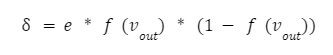
Якщо подивитися на формулу, то можна побачити, що вихідне значення останнього нейрона f(v_out) — це і є y, тобто значення функції активації від суми v_out. Тому формула набуває простого вигляду:

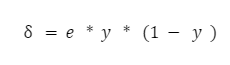
Тепер у нас є все, що потрібно, щоб обчислити корекцію ваги для останнього шару. Обчислюємо їх за такою формулою:

І друга вага:

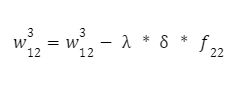
Параметр λ — це крок навчання нейронної мережі. Чим меншим ми його візьмемо, тим повільніше відбуватиметься процес навчання мережі. Він вибирається експериментально (наприклад, 0.1, 0.01, 0.001 і так далі), поки результат не буде задовільним.

Далі переходимо до наступного з кінця шару — і для цих нейронів також повторимо процедуру корекції ваги, використовуючи той же метод. Обчислимо значення їхніх локальних градієнтів:

Далі коригуємо вхідні зв'язки цих нейронів за відомою формулою з кроком навчання нейронної мережі. Для першого:

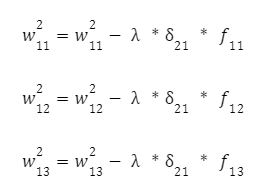
І для іншого нейрона:

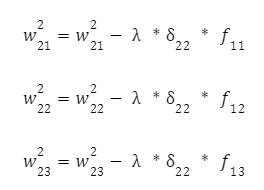
Залишилося скоригувати ваги першого шару. Знову обчислюємо локальний градієнт першого прихованого шару. Оскільки нейрони мають два виходи, спочатку обчислюємо виважену суму від кожного виходу:

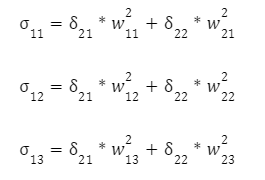
А вже потім множимо ці суми на похідну функції активації:

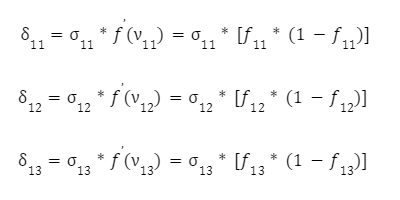
Залишилося скоригувати ваги першого шару:

Ми завершили першу ітерацію алгоритму, відкоригувавши всі ваги нейронної мережі. Щоб зробити другу, третю і так далі ітерації — потрібно взяти інший навчальний вектор вхідних значень (x1, x2) та пройтися мережею ще раз. З кожним наступним проходом ваги будуть скориговані дедалі точніше.

Мета алгоритму градієнтного спуску: мінімізувати критерій якості нейронної мережі — суму квадратів помилки навчальної вибірки:

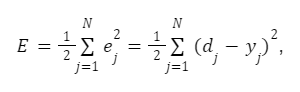
де N — число ітерацій.

Навчання нейронної мережі на Python

Код нижче представляє просту нейронну мережу з одним прихованим шаром, яка навчається з використанням градієнтного спуску. Працює він так:

• Під'єднуємо бібліотеку NumPy для роботи з масивами.
• Визначаємо дві функції: f(x) і df(x). Перша є сигмоїдною функцією активації, друга обчислює похідну цієї функції.
• Задаємо матриці ваг W1 і W2 (ваги між вхідним шаром та прихованим шаром — і між прихованим шаром та вихідним шаром відповідно).
• Визначаємо функцію go_forward(inp), ка виконує пряме поширення сигналу через мережу. Вхідний сигнал (inp) множиться на матрицю ваг W1, застосовується функція активації, потім результат множиться на матрицю ваг W2 та знову проганяється через функцію активації. Повертається вихідне значення нейронної мережі y і значення активацій прихованого шару out.
• Визначаємо функцію train(epoch), яка виконує навчання нейронної мережі. Усередині цієї функції відбувається ітеративне оновлення ваги з використанням градієнтного спуску. Для кожного циклу навчання обирається випадковий вхідний сигнал x із навчальної вибірки epoch. Потім виконується пряме поширення сигналу через мережу за допомогою функції go_forward, обчислюємо помилку e між вихідним та очікуваним значенням, за допомогою похідної функції активації визначаємо градієнти. За допомогою формул градієнтного спуску оновлюємо ваги W2 і W1.
• Генеруємо навчальну вибірку epoch, яка являє собою набір вхідних та вихідних значень для навчання мережі.
• Викликаємо функцію train(epoch) для навчання нейронної мережі на заданій вибірці.
• Далі відбувається пряме поширення сигналу через навчену мережу для кожного елемента в навчальній вибірці epoch, виводиться вихідне значення нейронної мережі y та очікуване значення x[−1].

import numpy as np # Під'єднуємо NumPy для роботи з масивами

def f(x): # Визначаємо сигмоїдну функцію активації 
    return 2/(1 + np.exp(-x)) — 1

def df(x): # Розраховуємо похідну сигмоїдної функції
    return 0.5 * (1 + x) * (1 — x)

W1 = np.array([[-0.2, 0.3, -0.4], [0.1, -0.3, -0.4]])
W2 = np.array([0.2, 0.3])

def go_forward(inp):
    sum = np.dot(W1, inp)
    out = np.array([f(x) for x in sum])

    sum = np.dot(W2, out)
    y = f(sum)
    return (y, out)

def train(epoch):
    global W2, W1
    lmd = 0.001
    N = 100000
    count = len(epoch)
    for k in range(N):
        x = epoch[np.random.randint(0, count)]
        y, out = go_forward(x[0:3])
        e = y — x[-1]
        delta = e * df(y)
        W2[0] = W2[0] — lmd * delta * out[0]
        W2[1] = W2[1] — lmd * delta * out[1]

        delta2 = W2 * delta * df(out)

        W1[0, :] = W1[0, :] — np.array(x[0:3]) * delta2[0] * lmd
        W1[1, :] = W1[1, :] — np.array(x[0:3]) * delta2[1] * lmd

epoch = [(-1, -1, -1, -1),
         (-1, -1, 1, 1),
          (1, 1, -1, -1),
         (-1, 1, -1, -1),
         (-1, 1, 1, -1),
         (1, -1, -1, -1),
         (1, -1, 1, 1),
         (1, 1, 1, -1)]
train(epoch)

for x in epoch:
    y, out = go_forward(x[0:3])
    print(f'Вихідне значення нейронної мережі: {y} => {x[-1]}')

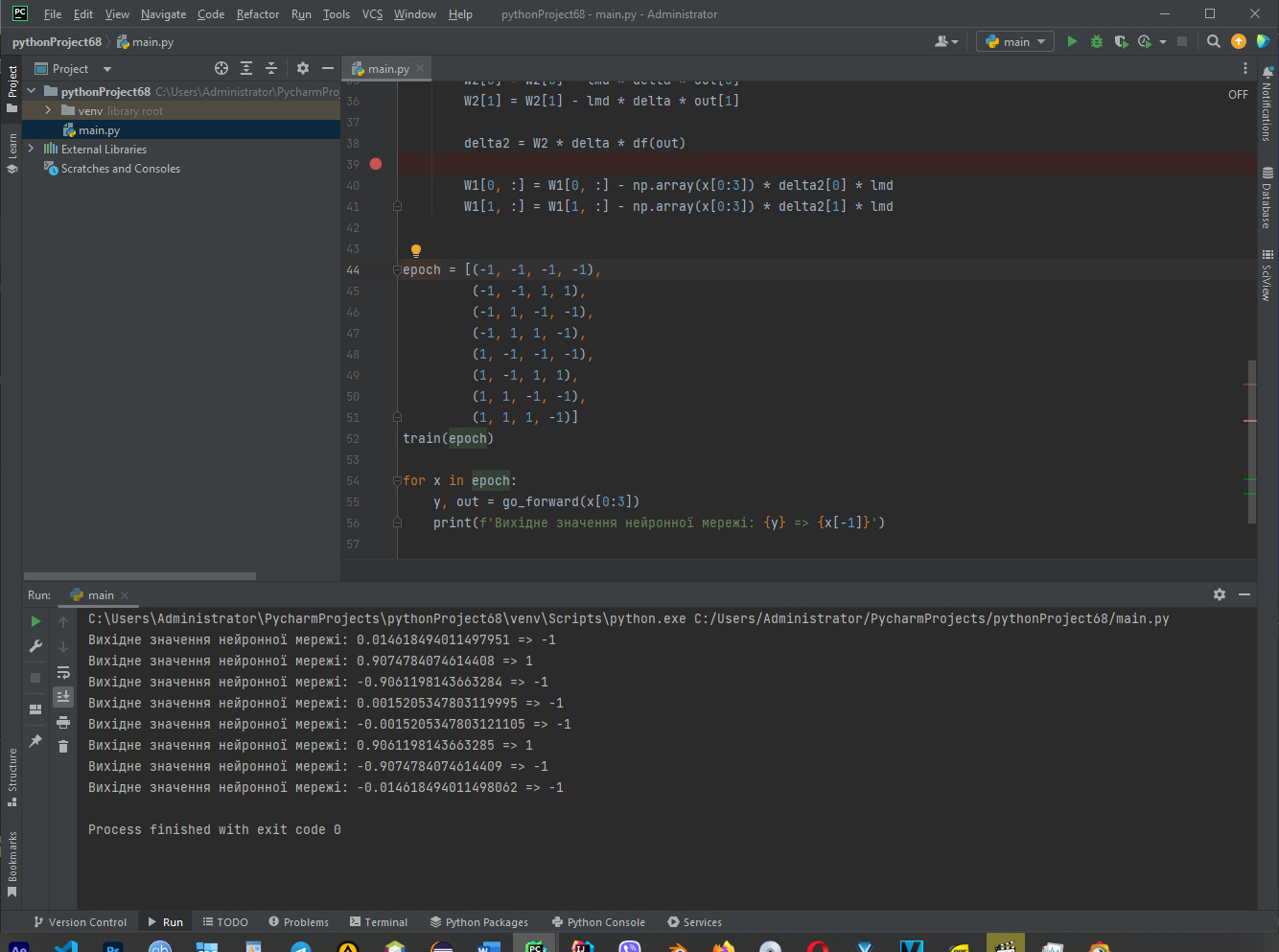
Результат роботи коду

Висновок

Якщо у вас залишилися труднощі з розумінням градієнтного спуску, уявіть собі ущелину з великою кількістю каміння, в яку скочується кулька. Вона котиться на саме дно випадковою траєкторією, вдаряючись об випадкові западини та виступи. Процес навчання нейронної мережі можна сприймати як спуск цієї кульки: чим довше вона падає, тим ближче вона до мінімуму функції.

Кулька, яка скочується вниз, представляє параметри моделі нейронної мережі, а її шлях вниз ущелиною відповідає зміні параметрів моделі за допомогою градієнтного спуску.

У процесі спуску кулька стикається з різними перешкодами на своєму шляху, які можуть бути аналогічними локальним мінімумам функції помилки. Чим довше кулька скочується, тим ближче вона може підійти до найглибшого місця ущелини, що відповідає мінімізації функції помилки та досягненню оптимальних значень параметрів моделі нейронної мережі.

Найскладніше — підібрати крок навчання, щоб градієнтний спуск не розходився і не забирав надто багато часу. Іноді градієнти, що передаються вагам мережі, можуть стати дуже малими або дуже великими, що ускладнює оновлення ваг і уповільнює збіжність алгоритму. У таких ситуаціях застосовують різні методи нормалізації та ініціалізації ваги, використовують добір функцій активації.