Градиентный спуск: алгоритм и пример на Python

Градиентный спуск — это один из методов оптимизации, который позволяет нейронной сети обучаться. О том, как он работает и почему сеть начинает «понимать», что правильно, а что нет, — читайте в этом материале.

Как обучают нейронки и зачем нужен градиентный спуск

Необученная нейронная сеть — плохой помощник: она ведет себя непредсказуемо и генерирует случайные ответы. Но если «подсказать» ей, что правильно, а что нет, она сможет делать прогнозы даже точнее, чем человек.

Но как именно этого достичь?

По умолчанию сигнал в нейронке передается от входных рецепторов в первый и все последующие скрытые слои, пока не трансформируется в сигнал для выходного слоя. Но пока параметры модели — значения весов и величина смещения нейронов — не настроены, мы будем получать некоторую ошибку. Чтобы ее минимизировать, нужно оптимизировать сеть.

Конечная цель оптимизации — найти такие значения параметров, при которых функция ошибки достигнет своего минимума.

Один из основных методов оптимизации, которые используются для достижения этой цели, — метод градиентного спуска. Он помогает находить направление, в котором функция ошибки уменьшается, и обновлять параметры модели соответствующим образом.

Градиентный спуск

Чтобы понять суть метода, вспомним математику.

Градиент — это вектор, который направлен в сторону максимального изменения функции.

В контексте нейронных сетей градиент функции ошибки помогает определить, как изменение того или иного параметра влияет на значение функции ошибки. Другими словами, он указывает, как нужно изменить параметры модели, чтобы ошибку сделать меньше.

Метод задействует вектор градиента для определения направления, в котором функция ошибки уменьшается быстрее всего. Это позволяет нам как бы «спускаться по склону ошибки», приближаясь к минимальному значению функции. Параметры модели обновляются на каждой итерации и двигаются в направлении, противоположном градиенту функции ошибки, пока мы не найдем точку в пространстве параметров, где ошибка на обучающих данных будет минимальной.

Начиная с некоторых начальных значений параметров, мы вычисляем градиент функции ошибки по этим параметрам. Затем мы изменяем значения параметров, вычитая некоторую долю градиента. Процесс циклично повторяется до тех пор, пока значения параметров не станут оптимальными или пока функция ошибки не перестанет значительно уменьшаться.

Алгоритм градиентного спуска

Математически градиентный спуск можно представить так:

1. Инициализировать параметры модели случайными значениями.

2. Подать входные данные в модель и получить предсказания.

3. Вычислить значение функции ошибки, сравнив предсказания с фактическими значениями. Как именно — зависит от конкретной задачи. Например, в задачах регрессии можно использовать формулу:

где n — количество примеров в обучающей выборке, y — фактическое значение, Y — предсказанное значение целевой переменной.

4. Определить градиент функции ошибки по каждому параметру модели. Формула выбирается в зависимости от выбранной функции ошибки.

5.Обновить значения параметров по формуле:

новое значение параметра = старое значение параметра − learning rate * градиент.

Learning rate (скорость обучения) — это гиперпараметр, который контролирует скорость сходимости алгоритма градиентного спуска и определяет размер шага, с которым обновляются параметры модели. Чем меньше шаг — тем больше времени понадобится на обучение нейронной сети и обновление параметров.

6. Повторить шаги 2–5 для каждого этапа прогонки обучения (эпохи) или до достижения критерия остановки.

Пример коррекции весов нейронной сети

Допустим, у нас есть полносвязная нейронная сеть прямого распространения. У нее есть веса связи (выбраны случайно), и они лежат в диапазоне значений [−0.5;0.5].

Полносвязная нейронная сеть прямого распространения

Верхний индекс означает принадлежность к тому или иному слою. У каждого нейрона есть активационная функция f(x). У каждого наблюдения есть свой отклик — d.

Проходя по этой сети, мы получаем вектор наблюдений:

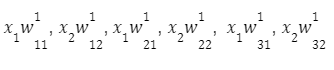
Для первого узла первого слоя получаем:

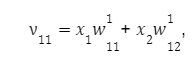
для второго:

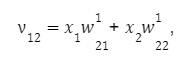
для третьего:

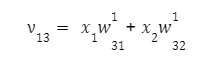
Проходя по сети, на выходе нейрона мы будем иметь некоторое значение, полученное через функцию активации. Оно будет вычислено по формуле:

Передвигаясь далее по сети, мы получаем вектор наблюдений:

Для каждого нейрона второго слоя:

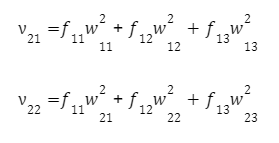
На первом нейроне второго слоя:

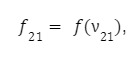
на втором:

Аналогично доходим до выходного значения y. Поскольку мы знаем желаемое выходное значение для нашего вектора x1 и x2 — d, несложно подсчитать ошибку на выходе:

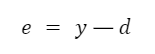
С этого момента начинается процесс корректировки весов. Она выполняется в обратном направлении, с выхода на вход. Согласно алгоритму backpropagation мы должны вычислить локальный градиент для выходного нейрона. Делается это по формуле:

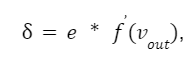
где f(v_out) — производная функции активации выходного нейрона.

Выходной функцией активации может быть или гиперболический тангенс, или сигмоида.

Читайте также Полный гайд по функциям активации нейронных сетей

Эти функции отличаются лишь уровнем (для гиперболического тангенса это диапазон от −1 до 1, а для логистической функции — промежуток от −0.5 до 0,5).

Предположим, мы выбрали функцию:

Ее производная будет выглядеть как:

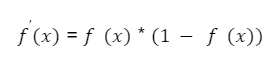
А локальный градиент можно вычислить как:

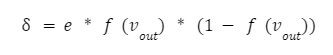
Если посмотреть на формулу, можно увидеть, что выходное значение последнего нейрона f(v_out) — это и есть y, то есть значение функции активации от суммы v_out. Поэтому формула приобретает простой вид:

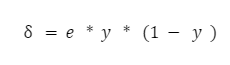
Теперь у нас есть все что нужно, чтобы вычислить коррекцию весов для последнего слоя. Вычисляем их по следующей формуле:

И второй вес:

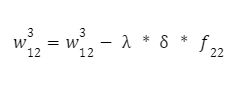
Параметр λ — это шаг обучения нейронной сети. Чем меньше мы его возьмем, тем медленнее будет происходить процесс обучения сети. Он выбирается экспериментально (например, 0.1, 0.01, 0.001 и так далее), пока результат не будет удовлетворительным.

Далее переходим к следующему с конца слоя — и для этих нейронов также повторим процедуру коррекции весов, используя тот же метод. Вычислим значения их локальных градиентов:

Далее корректируем входные связи этих нейронов по уже известной формуле с шагом обучения нейронной сети. Для первого:

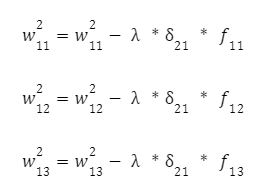
И для другого нейрона:

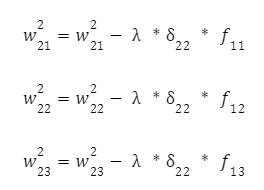
Осталось скорректировать веса первого слоя. Снова вычисляем локальный градиент первого скрытого слоя. Так как нейроны имеют два выхода, сначала вычисляем взвешенную сумму от каждого выхода:

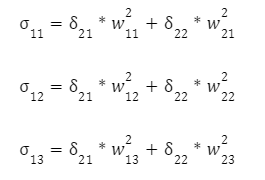
А уже затем умножаем эти суммы на производную функции активации:

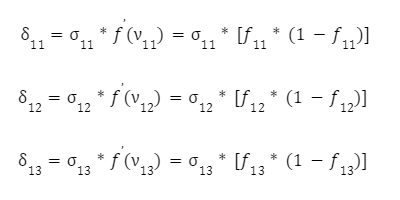
Осталось скорректировать веса первого слоя:

Мы завершили первую итерацию алгоритма, откорректировав все веса нейронной сети. Чтобы сделать вторую, третью и так далее итерации — нужно взять другой обучающий вектор входных значений (x1, x2) и пройтись по сети еще раз. С каждым последующим проходом веса будут скорректированы все точнее и точнее.

Цель алгоритма градиентного спуска: минимизировать критерий качества нейронной сети — сумму квадратов ошибки обучающей выборки:

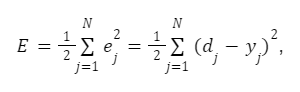
где N — число итераций.

Обучение нейронной сети на Python

Код ниже представляет простую нейронную сеть с одним скрытым слоем, которая обучается с использованием градиентного спуска. Работает он так:

• Подключаем библиотеку NumPy для работы с массивами.
• Определяем две функции: f(x) и df(x). Первая представляет собой сигмоидную функцию активации, вторая вычисляет производную этой функции.
• Задаем матрицы весов W1 и W2 (веса между входным слоем и скрытым слоем — и между скрытым слоем и выходным слоем соответственно).
• Определяем функцию go_forward(inp), которая выполняет прямое распространение сигнала через сеть. Входной сигнал (inp) умножается на матрицу весов W1, применяется функция активации, затем результат умножается на матрицу весов W2 и снова прогоняется через функцию активации. Возвращается выходное значение нейронной сети y и значения активаций скрытого слоя out.
• Определяем функцию train(epoch), которая выполняет обучение нейронной сети. Внутри этой функции происходит итеративное обновление весов с использованием градиентного спуска. Для каждого цикла обучения выбирается случайный входной сигнал x из обучающей выборки epoch. Затем выполняется прямое распространение сигнала через сеть с помощью функции go_forward, вычисляем ошибку e между выходным и ожидаемым значением, с помощью производной функции активации определяем градиенты. С помощью формул градиентного спуска обновляем веса W2 и W1.
• Генерируем обучающую выборку epoch, которая представляет собой набор входных и выходных значений для обучения сети.
• Вызываем функцию train(epoch) для обучения нейронной сети на заданной выборке.
• Далее происходит прямое распространение сигнала через обученную сеть для каждого элемента в обучающей выборке epoch, выводится выходное значение нейронной сети y и ожидаемое значение x[−1].

import numpy as np # Подключаем NumPy для работы с массивами

def f(x): # Определяем сигмоидную функцию активации 
    return 2/(1 + np.exp(-x)) — 1

def df(x): # Рассчитываем производную сигмоидной функции
    return 0.5 * (1 + x) * (1 — x)

W1 = np.array([[-0.2, 0.3, -0.4], [0.1, -0.3, -0.4]])
W2 = np.array([0.2, 0.3])

def go_forward(inp):
    sum = np.dot(W1, inp)
    out = np.array([f(x) for x in sum])

    sum = np.dot(W2, out)
    y = f(sum)
    return (y, out)

def train(epoch):
    global W2, W1
    lmd = 0.001
    N = 100000
    count = len(epoch)
    for k in range(N):
        x = epoch[np.random.randint(0, count)]
        y, out = go_forward(x[0:3])
        e = y — x[-1]
        delta = e * df(y)
        W2[0] = W2[0] — lmd * delta * out[0]
        W2[1] = W2[1] — lmd * delta * out[1]

        delta2 = W2 * delta * df(out)

        W1[0, :] = W1[0, :] — np.array(x[0:3]) * delta2[0] * lmd
        W1[1, :] = W1[1, :] — np.array(x[0:3]) * delta2[1] * lmd

epoch = [(-1, -1, -1, -1),
         (-1, -1, 1, 1),
          (1, 1, -1, -1),
         (-1, 1, -1, -1),
         (-1, 1, 1, -1),
         (1, -1, -1, -1),
         (1, -1, 1, 1),
         (1, 1, 1, -1)]
train(epoch)

for x in epoch:
    y, out = go_forward(x[0:3])
    print(f'Выходное значение нейронной сети: {y} => {x[-1]}')

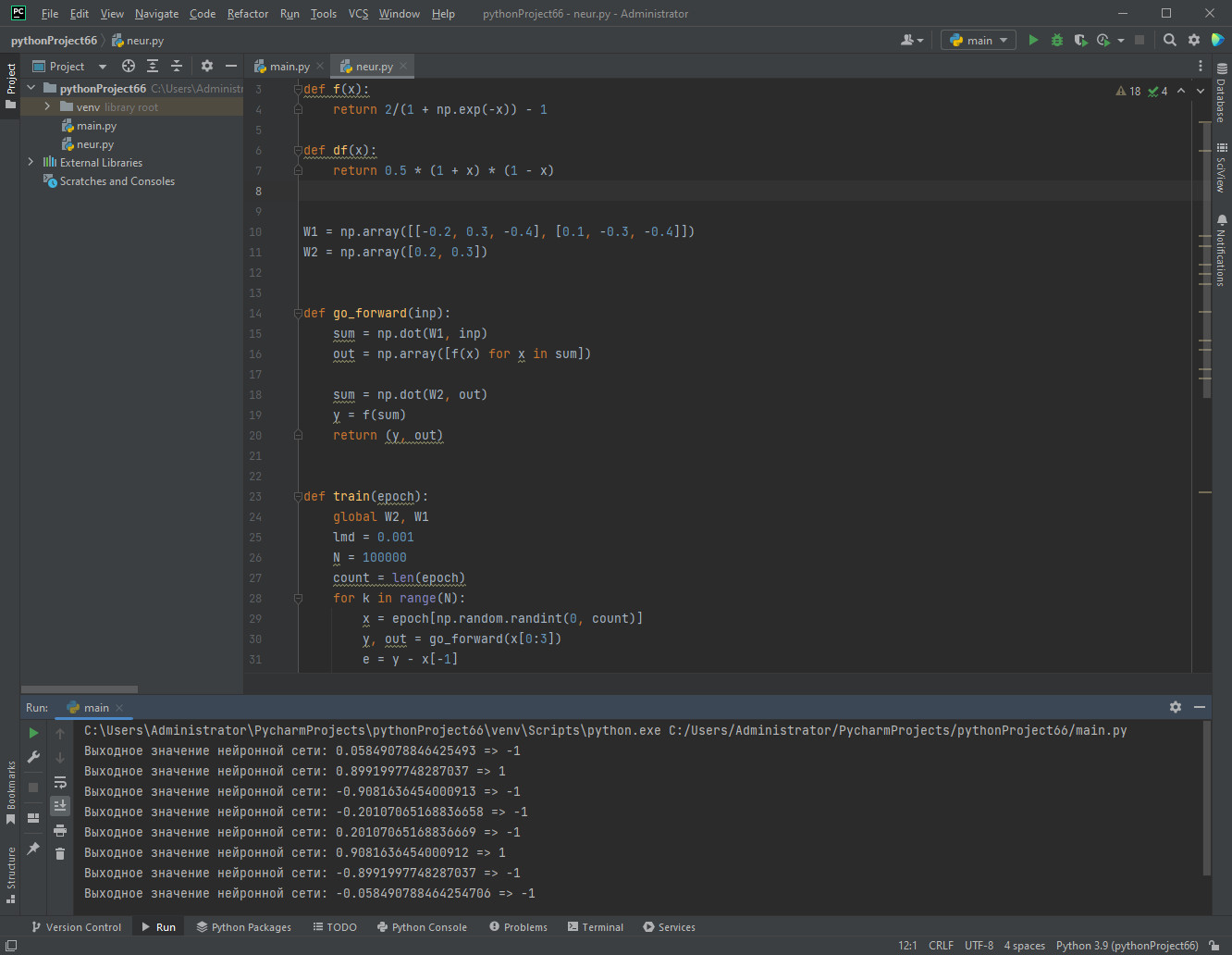
Результат работы кода

Заключение

Если у вас остались трудности с пониманием градиентного спуска, представьте себе ущелье с большим числом камней, в которое скатывается шарик. Он катится на самое дно по случайной траектории, ударяясь о случайные впадины и выступы. Процесс обучения нейронной сети можно воспринимать как спуск этого мячика: чем дольше он падает, тем ближе он к минимуму функции.

Шарик, который скатывается вниз, представляет параметры модели нейронной сети, а его путь вниз по ущелью соответствует изменению параметров модели с помощью градиентного спуска.

В процессе спуска шарик сталкивается с различными преградами на своем пути, которые могут быть аналогичными локальным минимумам функции ошибки. Чем дольше шарик скатывается, тем ближе он может подойти к самому глубокому месту ущелья, что соответствует минимизации функции ошибки и достижению оптимальных значений параметров модели нейронной сети.

Самое сложное — подобрать шаг обучения, чтобы градиентный спуск не расходился и не отнимал слишком много времени. Иногда значения градиентов, передаваемых весам сети, могут стать очень малыми или очень большими, что затрудняет обновление весов и замедляет сходимость алгоритма. В таких ситуациях применяют различные методы нормализации и инициализации весов, используют подбор функций активации.