Функції активації: Ступінчаста, лінійна, сигмоїда, ReLU та Tanh

Нейронні мережі працюють, як людський мозок. Вони отримують певні дані (вхід/input), обробляють їх у декілька етапів (приховані шари / hidden layers), а потім видають результат (вихід/output). 

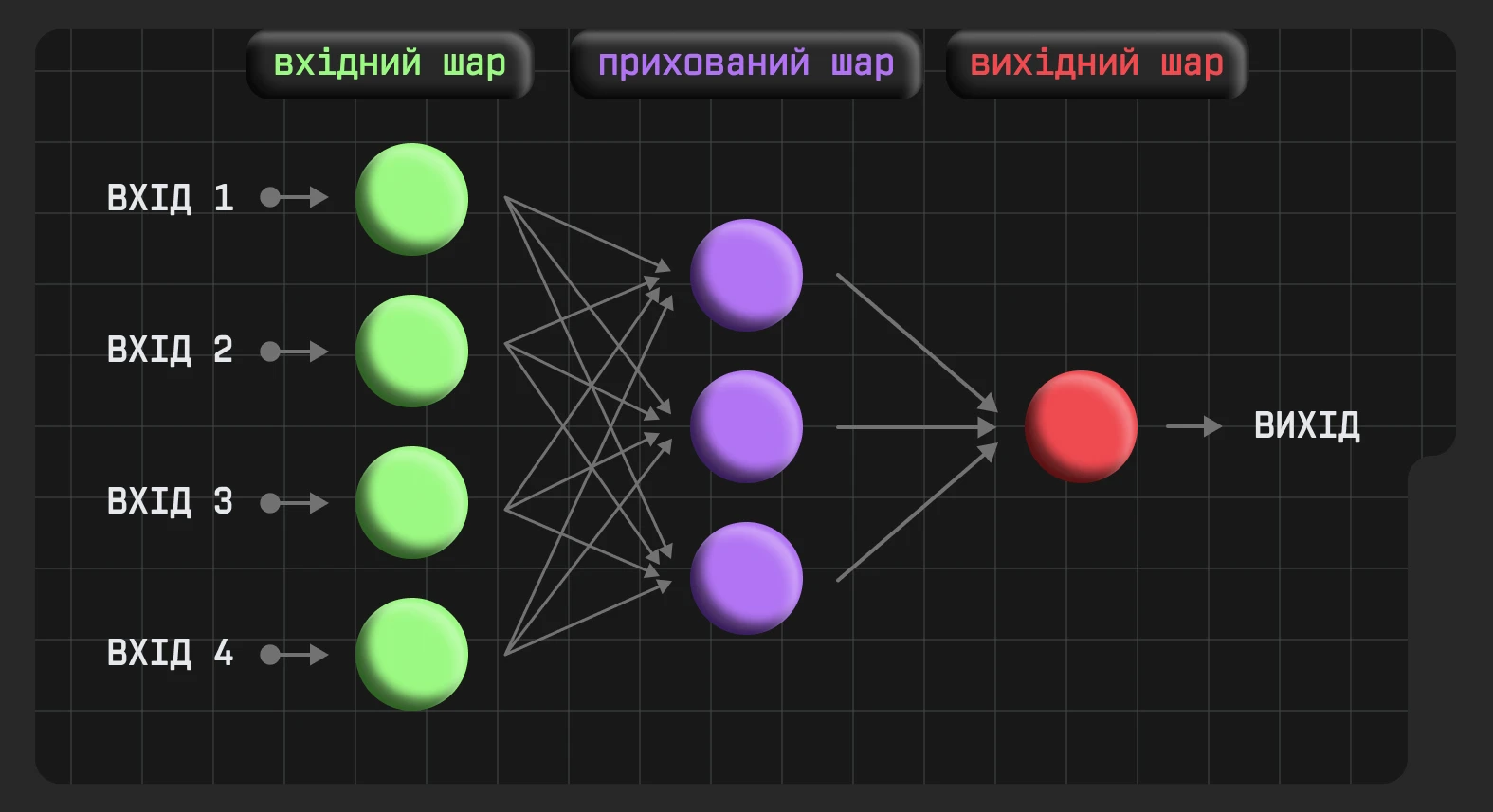
Використання нейронних мереж може бути пов’язаним із різними завданнями: 

1. Класифікація.
2. Розпізнавання зображень. 
3. Обробка природної мови. 
4. Передбачення та прогнозування. 
5. Генерація зображень, текстів, музики й відео.
6. Системи рекомендацій і персоналізація. 

Наприклад, потрібно створити просту нейромережу, яка вирішує, чи є сприятливі умови для того, щоб піти в похід у гори. Для цього беремо до уваги 4 фактори: дощ, температура повітря, сила вітру та кількість інших туристів у кемпінгах. 

Якщо будь-який із цих факторів задовільний для походу, то його значення дорівнює одиниці, якщо ні — нулю. Кожен із цих чинників також може мати ступінь важливості для ухвалення рішення, тому присвоїмо їм значення від 1 до 5. Ці значення — коефіцієнти для рівняння, результат якого визначить, чи варто вирушати в подорож. 

Гіпотетично, для групи туристів дощ буде найважливішим складником, тому цей показник дорівнює п’яти. Сила вітру також має вагоме значення для гірського походу, встановимо 4 для цього чинника. Температура повітря та наявність інших туристів набагато менше впливають на рішення, тому ці фактори отримують значення 2.

Загальна формула функції для нейромережі має такий вигляд: 

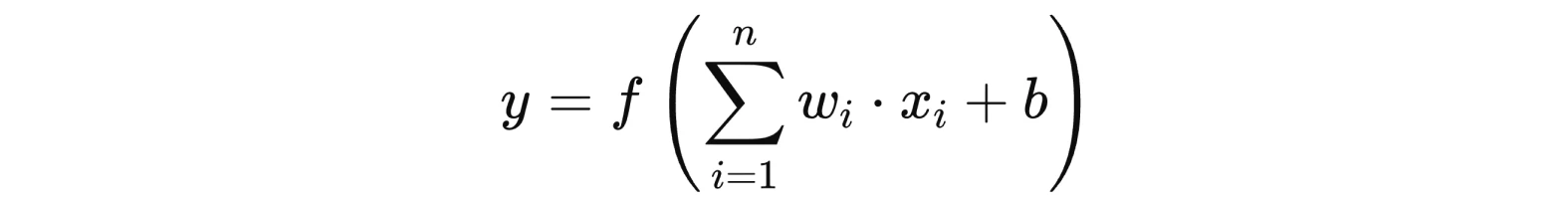
x₁​,x₂​,…,x_n — фактори 
w₁​,w₂​,…,w_n​ — ваговий коефіцієнт кожного фактору 
b — bias, або зміщення. 

Це додатковий параметр, який забезпечує гнучкість нейромережі. Він зсуває функцію у потрібному напрямку і дозволяє нейронам активуватися, навіть якщо сума не є позитивною. Зміщення визначають під час навчання нейронної мережі, але його початкове значення можна встановити випадковим чином, бо воно все одно не може бути коректним до початку навчання моделі. 

f(.) — функція активації, яка визначає вихід. 

Рівняння для нейромережі для планування гірського походу: 

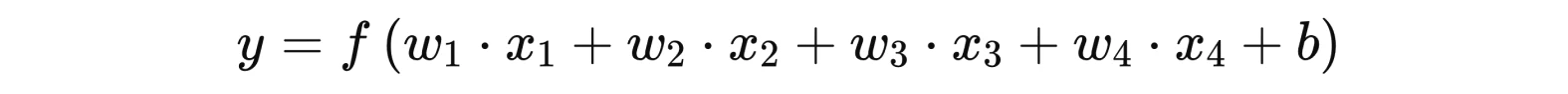
З визначеною вагою кожного фактору: 

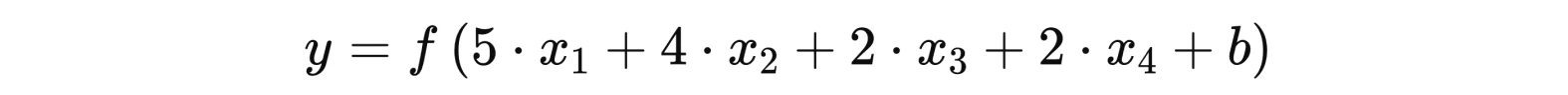
х₁ = 0, якщо буде дощ, і =1, якщо дощу не буде 
х₂ має певний діапазон сприятливої температури повітря (=1, якщо задане значення входить до нього і =0, якщо не входить)
х₃ також може мати діапазон для сили вітру і визначатися згідно з тією самою логікою
х₄ = 1, якщо кемпінги заповнені на менш як 90 %, та =0, якщо це значення більше

Ця нейромережа зможе давати відповідь «так» або «ні» на запитання, чи варто йти в похід, якщо туристи зможуть надати комбінацію даних, що потрібні для цієї моделі. Для розробки складнішої й точнішої нейромережі, яка передбачає умови для походу, вже потрібно буде використовувати декілька прихованих шарів та нелінійні функції активації. 

Активація нейрона 

Кожен нейрон отримує дані або від вхідної інформації, або від попереднього шару нейронів у вигляді числових значень. Потім вони множаться на свою вагу, яка визначає зв’язок між нейронами. Всі зважені сигнали, отримані нейронами, підсумовуються (за потреби зі зміщенням) і активуються за допомогою функції, якщо вона має значення більше нуля. Після цього нейрони передають вихідні сигнали далі мережею до наступного шару або виходу. 

Навіщо активується нейрон?

Насамперед активація нейрона потрібна, щоб він зміг передавати дані у вигляді вихідного сигналу, що забезпечує роботу нейромережі. Система влаштована так, що не всі нейрони мають бути активованими, але саме активовані визначають відповідь нейромережі на запит. 

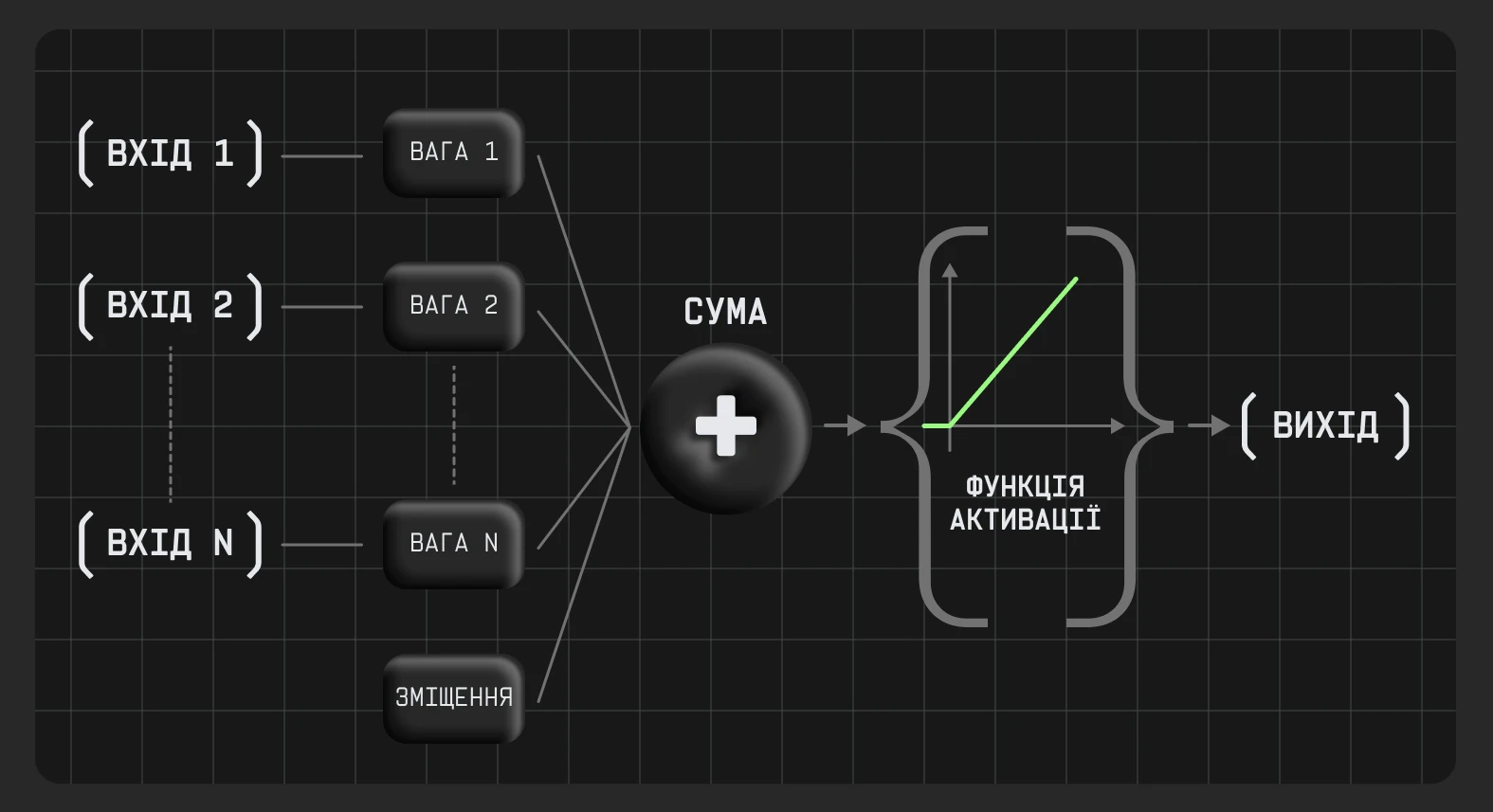
Що таке функція активації

Функція активації оцінює, чи має нейрон бути «запущеним». Це математична функція, яка визначає вихід нейрона на основі його входу.

Функції активації потрібні для нейронних мереж, оскільки без них вихід моделі був би просто лінійною функцією входу. Іншими словами, нейронні мережі не зможуть обробляти великі обсяги даних. Основна мета — створити нелінійність моделі, що дасть змогу нейромережі працювати зі складними залежностями й патернами. 

Східчаста функція 

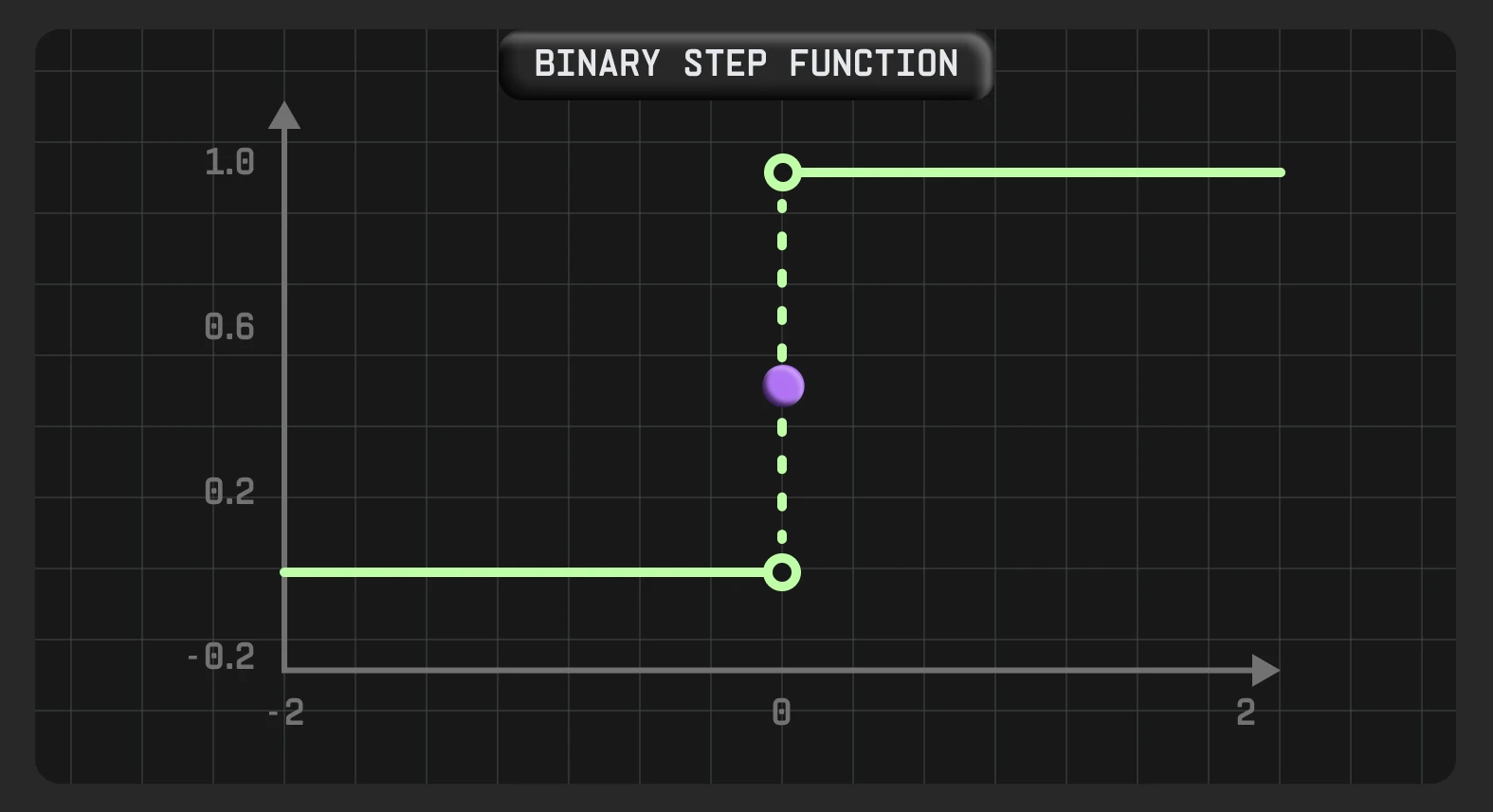
Східчаста функція — бінарна, одна із найпростіших функцій активації. Нейрон активується, якщо значення Y більше за певне порогове значення, тобто вихід дорівнює одиниці. Якщо Y менший за це порогове значення, то нейрон не буде активовано і його значення дорівнює нулю. Її часто використовують у задачах бінарної класифікації, де метою є класифікація вхідних даних за однією з двох категорій. Наприклад, визначити, чи температура в приміщенні є занадто низькою, щоб увімкнути опалення. 

Вона має такий вигляд: 

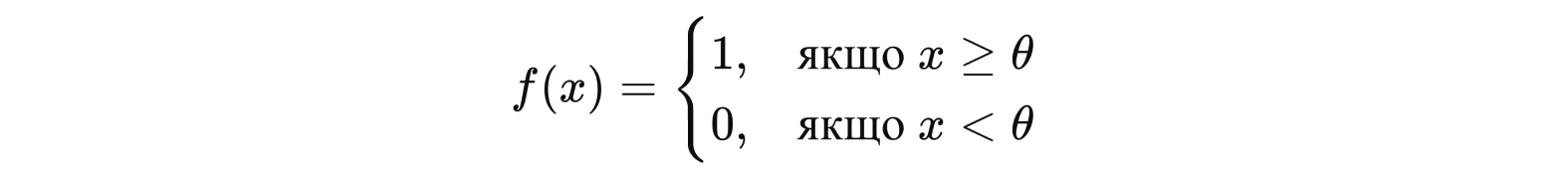
x — вхід нейрона 
θ — порогове значення

Переваги: ця функція легка для розуміння і реалізації, тому її часто використовують в освітніх цілях для вивчення принципів роботи нейронних мереж. 

Недоліки: не підходить для складних моделей, що потребують нелінійних зв’язків. 

Якщо треба створити нейромережу, яка визначає приналежність об’єкта до певного типу, але класифікація не обмежується лише двома, застосування східчастої функції активації буде проблематичним. Коли більш як один нейрон прийматиме значення 1, нейромережа не зможе визначити, до якого класу належить об’єкт. 

Лінійна функція 

Лінійну функцію активації також називають функцією без активації, оскільки за використання такої функції вихід завжди пропорційний входу. Таким чином, така функція надає зважену суму вхідних даних і повертає значення, подане в мережу, формуючи прямі зв’язки між входом і виходом. Вихід лінійної функції не обмежений кордонами. 

Одним із практичних прикладів застосування лінійної функції активації є прогнозування зміни цін за допомогою регресійної моделі на основі попередніх даних. 

Такий вигляд має лінійна функція активації:

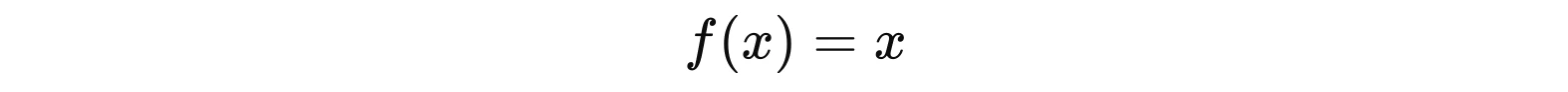
або

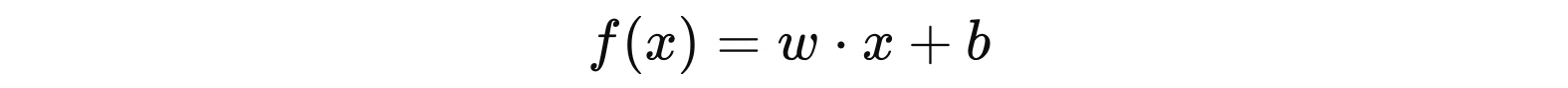
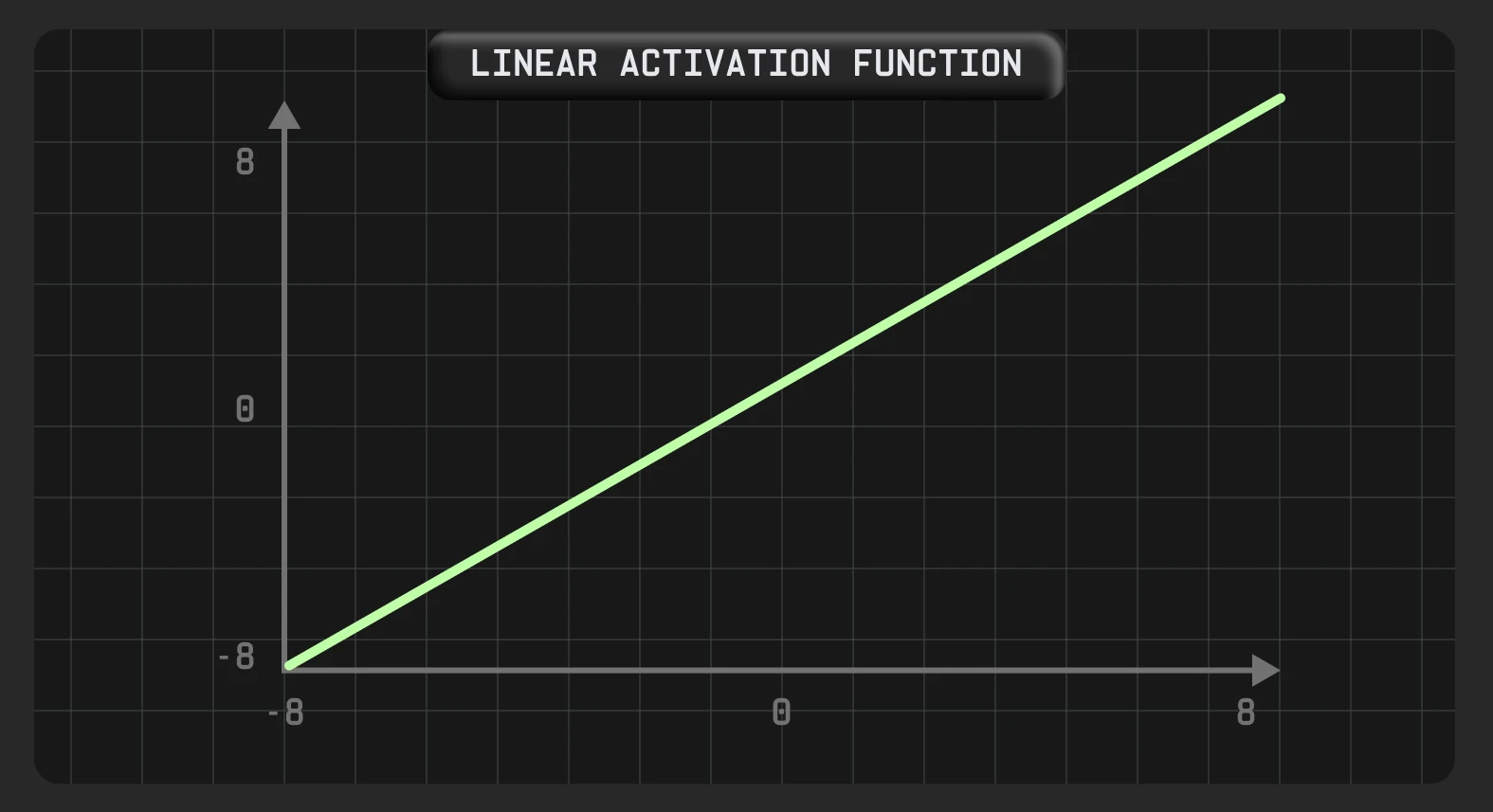
Переваги: так само, як і східчаста, лінійна функція активації проста для сприйняття і використання у простих моделях або навчальних цілях для демонстрації роботи нейромереж. 

Недоліки: оскільки ця функція також не вводить нелінійність в модель, вона не може бути ефективною для складних патернів. 

ReLu

ReLu (Rectified Linear Unit) — одна з найпопулярніших функцій активації в сучасних нейромережах, особливо якщо йдеться про глибокі нейронні мережі (DNNs), які мають велику кількість шарів між входом та виходом. Ця функція замінює всі від’ємні вхідні значення на 0 та не змінює позитивні значення. 

Функцію ReLU можна легко вважати майже лінійною функцією, і в певному сенсі це кусково-лінійна функція з двома лінійними частинами. Однак, оскільки вона має функцію похідної, її вважають нелінійною функцією активації й вона допускає зворотне розповсюдження помилок. 

Backpropagation (зворотне розповсюдження помилок) — один із головних алгоритмів, задіяних у навчанні нейромереж. Цей процес дає змогу коригувати зміщення та ваги на основі виявлених помилок у прогнозах. 

ReLu часто використовують у комп’ютерному зорі, щоб розпізнавати вміст зображення. Аналізуючи пікселі, з яких складається зображення, нейронна мережа може виділити основні риси, кольори та ключові риси об’єктів, щоб ідентифікувати об’єкт. 

Функція ReLU:

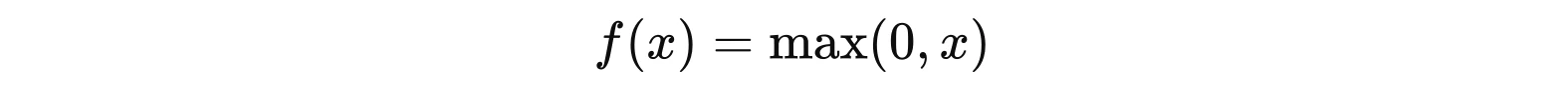
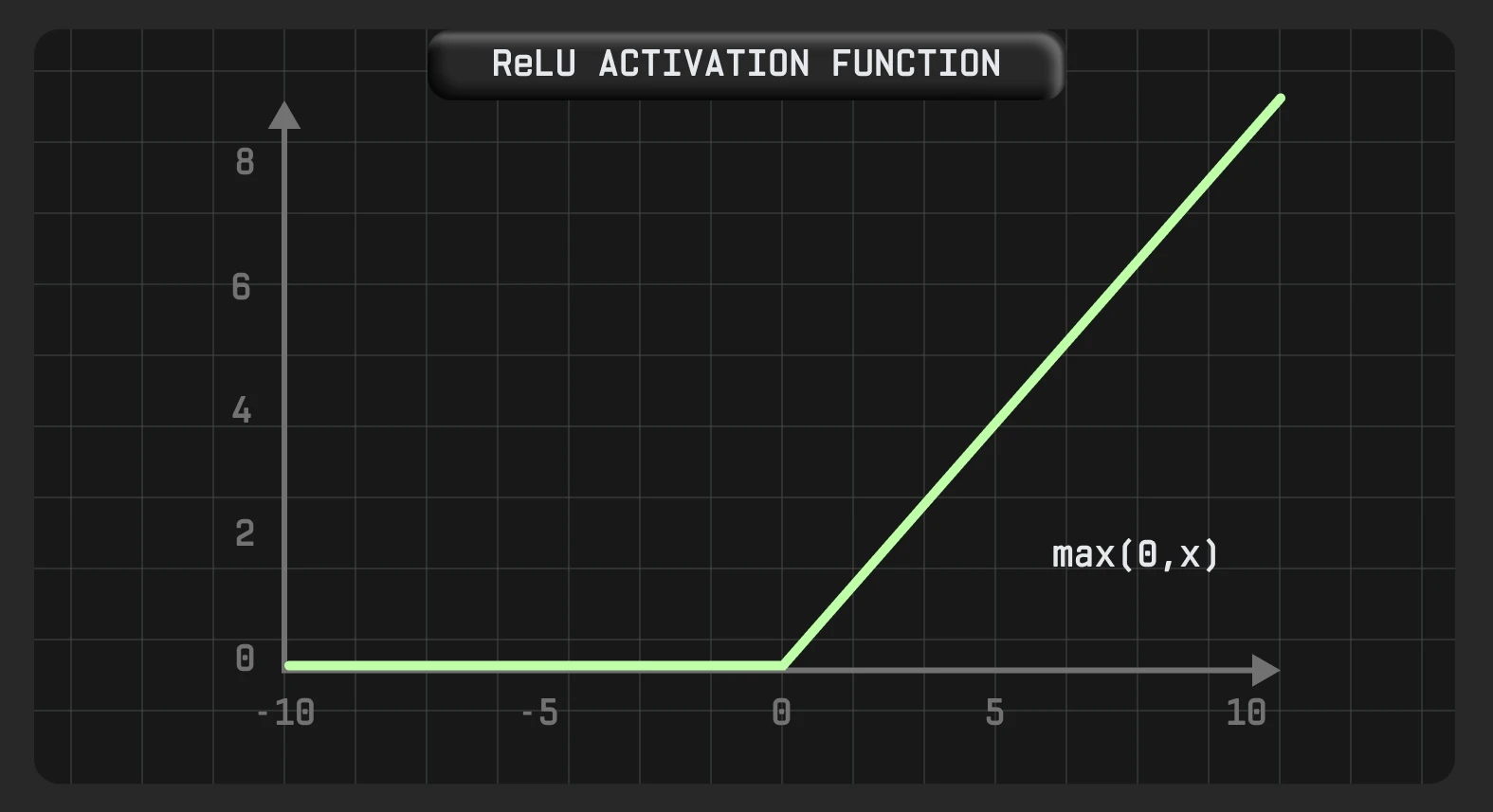
Переваги: ця функція дозволяє мережі бути обчислювально ефективною, утримуючи нейрони деактивованими, коли вхід менший за 0. Завдяки цьому модель також швидше навчається. 

Недоліки: проблема полягає в тому, що всі від’ємні значення відразу стають нульовими, що зменшує здатність моделі навчатися на основі даних. Це означає, що будь-який негативний вхід, наданий функції активації ReLU, одразу створює нульовий градієнт, що впливає на кінцевий графік, не відтворюючи від’ємні значення належним чином.

Leaky ReLU

Зважаючи на переваги ReLU, експерти працювали над проблемою нейронів, що вмирають, і розробили вдосконалену версію, відому як Leaky ReLU.

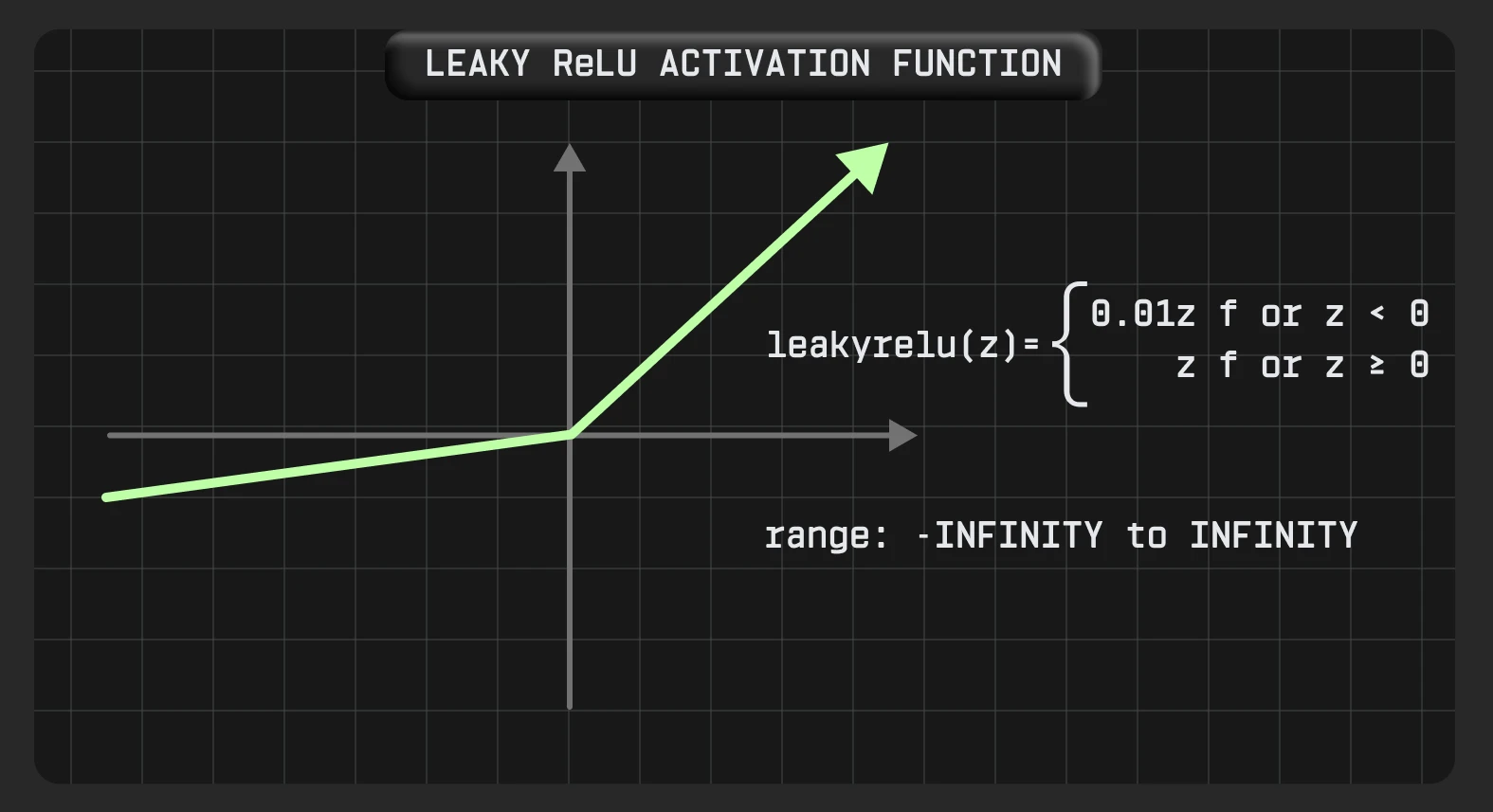
Leaky ReLU (Leaky Rectified Linear Unit) повертає ненульовий результат, а не від’ємні значення, що перетворюються на нуль (як у випадку з ReLU). Це допомагає збільшити діапазон функції ReLU. Зазвичай значення a становить 0,01 або близько того. 

Таким чином, замість попередньої горизонтальної лінії існує негоризонтальна похила лінія для негативної частини. Такий підхід розповсюджує зворотне поширення помилок для негативних вхідних значень, оминаючи проблему «мертвого нейрона».

Формула Leaky ReLU:  

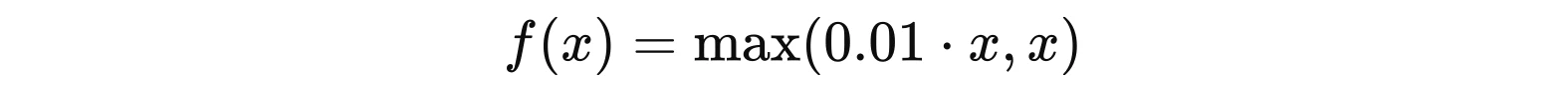
Сигмоїда 

Сигмоїда — поширена нелінійна функція активації, яку переважно використовують у машинному навчанні. Він може прийняти будь-яке дійсне значення та дає вихідні значення в діапазоні між 0 і 1, з більшим вхідним значенням, ближчим до 1, і меншим, ближчим до 0. 

Сигмоїда диференційована. Це означає, що ми можемо знайти нахил сигмоподібної кривої в будь-яких двох точках.

Тому цю функцію особливо часто використовують для моделей, де потрібно передбачити ймовірність як результат. Оскільки ймовірність будь-чого існує лише в діапазоні від 0 до 1, sigmoid є правильним вибором.

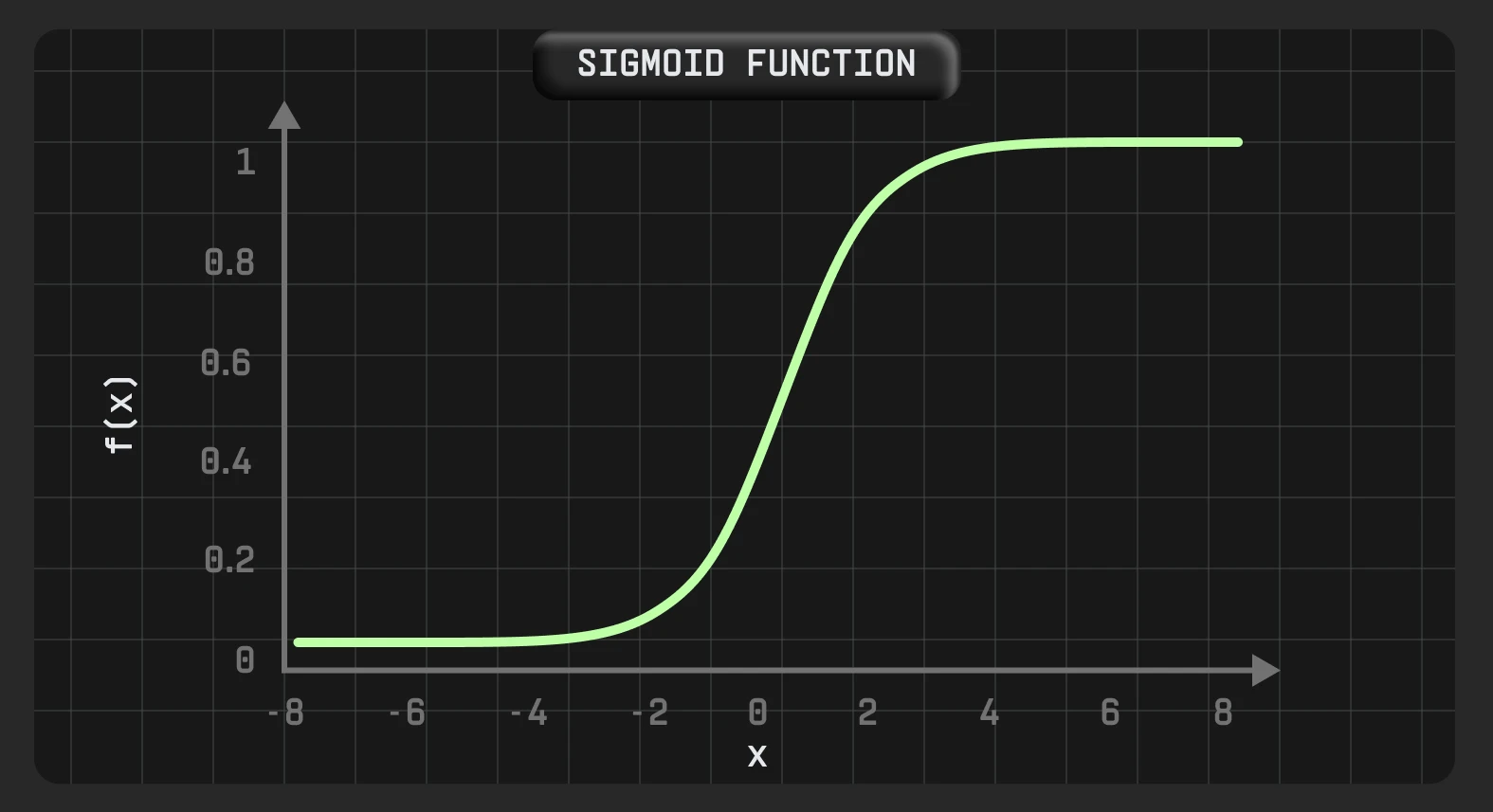
Крім того, важливою характеристикою сигмоїдної функції є те, що вона має тенденцію підштовхувати вхідні значення до будь-якого кінця кривої (0 або 1) завдяки своїй S-подібній формі. В області, близькій до нуля, якщо ми трохи змінимо вхідне значення, відповідні зміни на виході будуть дуже великими, і навпаки. 

Формула сигмоїди — S-подібна гладка функція, яка трохи нагадує східчасту:

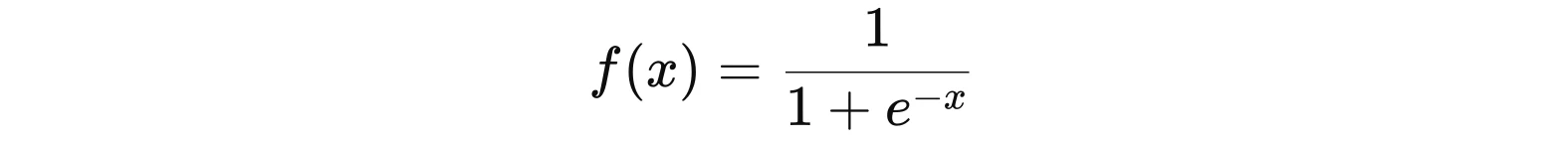
Переваги: як нелінійна функція активації сигмоїда може працювати зі складними закономірностями. 

Недоліки: діапазон від 0 до 1 не завжди актуальний для багатьох задач, тому використання цієї функції є відносно обмеженим. Також навчання мережі з функцією сигмоїдної активації є складним і нестабільним, бо вихідні дані такої функції не є симетричними навколо нуля, тому всі нейрони мають однаковий знак на виході.

Tahn

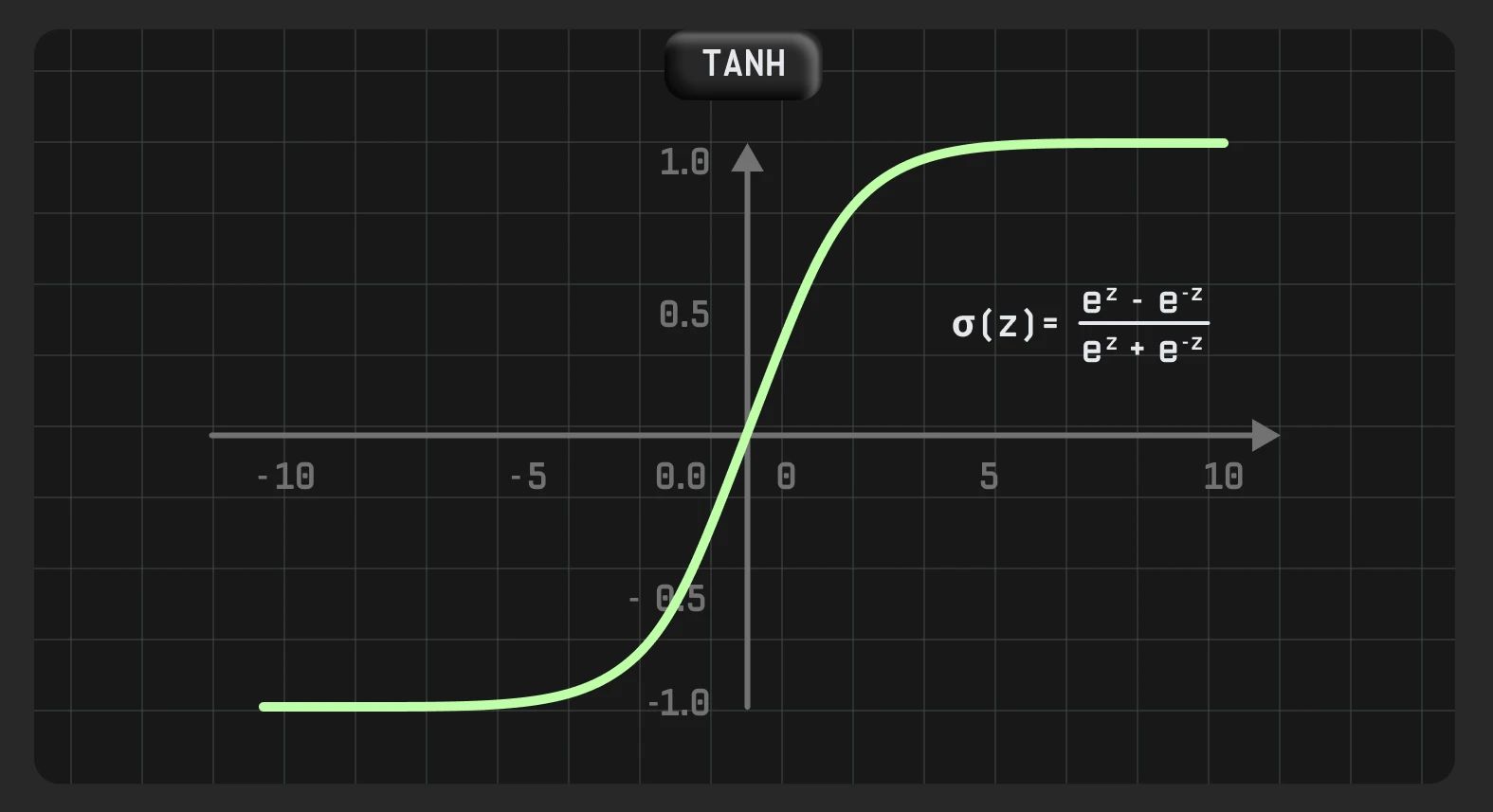
Tanh (гіперболічний тангенс) — це скоригована версія сигмоїди. Однак, на відміну від sigmoid, вихідний сигнал якого становить від 0 до 1, вихід tanh варіюється від -1 до 1. Більший вхідний сигнал ближче до 1, менший — ближче до -1.

Його зазвичай застосовують у прихованих шарах нейронної мережі, оскільки його значення перебуває в діапазоні від -1 до 1. Тому середнє значення для прихованого шару виходить рівним 0 або дуже близьким до нього. Отже, це допомагає центрувати дані, наближаючи середнє значення до 0. 

Градієнт tanh у чотири рази більший за градієнт сигмоїдної функції. Це означає, що використання функції активації tanh призводить до вищих значень градієнта під час навчання та більших оновлень вагових коефіцієнтів мережі.

Гіперболічний тангенс схожий на витягнуту сигмоїду: 

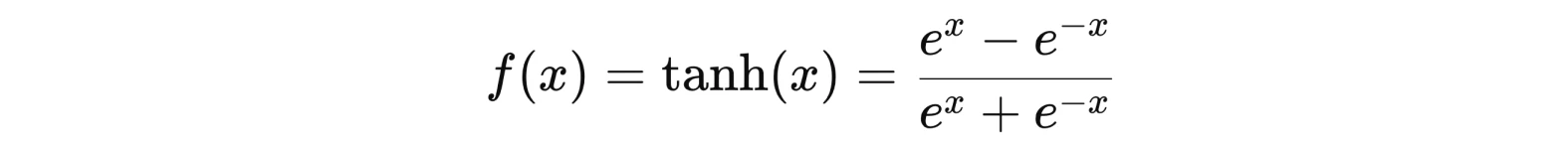
e — основа натурального логарифма

Переваги: має нульовий центр, що дозволяє градієнту рухатися в обох напрямках. Може легко відтворити вихідні дані великого позитивного або негативного значення.

Недоліки: ця функція має ту саму проблему градієнта, що зникає, як і сигмоїдна функція, але з градієнтом з більшою амплітудою. 

Softmax

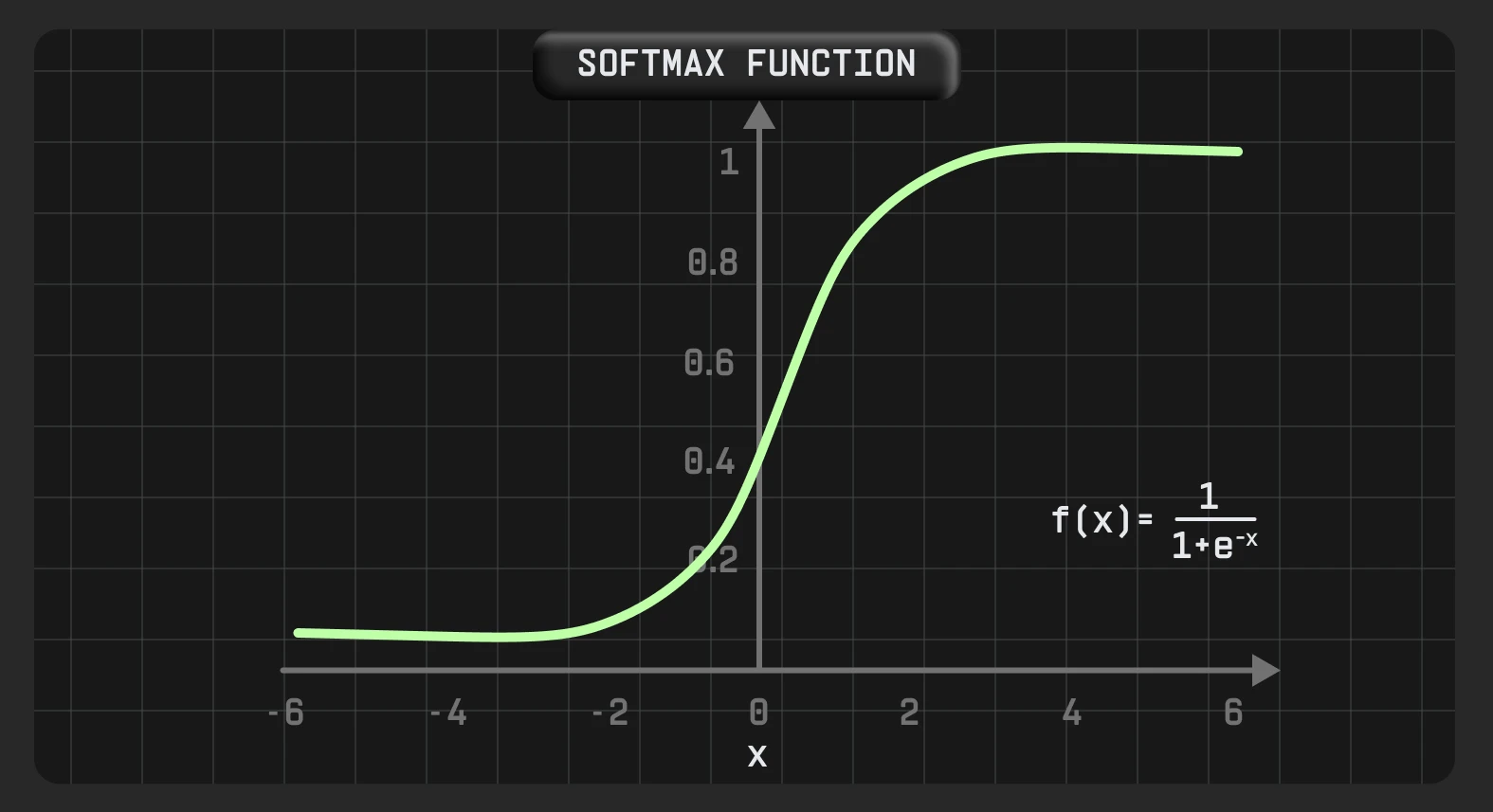
Softmax — це нелінійна функція, яку переважно використовують для класифікаційних задач. Вона перетворює набори чисел (логітів) на ймовірності. 

Softmax дає оцінку для вихідних даних для кожного класу між 0 і 1, а потім ділить їх на суму, щоб визначити ймовірність потрапляння вхідного значення до певних категорій. Ця функція найбільш поширена на вихідному рівні, зокрема для нейронних мереж, які потребують класифікації вхідних даних у кількох категоріях.

Наприклад, Softmax зручно використовувати для визначення приналежності контенту до якогось типу (об’єкта на зображенні, жанру музики, тексту або відео, виявлення теми тощо).

Формула Softmax: 

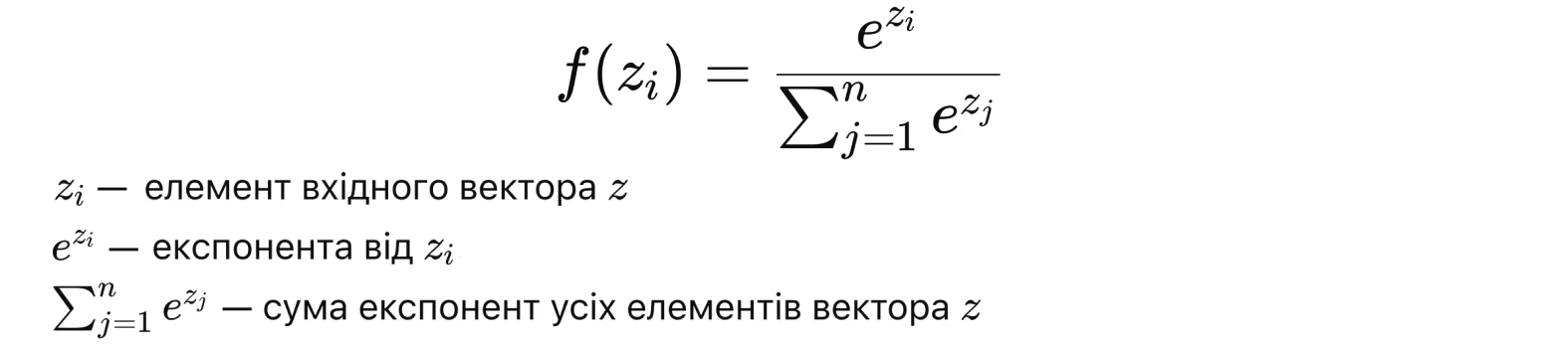
Переваги: імовірності легші для розуміння та інтерпретації в порівнянні з вихідними значеннями. Softmax забезпечує чітко визначений розподіл імовірностей для кожного класу, що дає змогу оцінити роботу нейромережі та її впевненість у прогнозах. Функція softmax також відносно чисельно стабільна, що робить її ефективною для навчання нейронних мереж.

Недоліки: підходить тільки для класифікації об’єктів, які належать тільки до одного з наявних класів, що обмежує застосування функції, якщо об’єкт представляє декілька категорій одночасно. Також модель може бути неточною під час роботи з великою кількістю класів, оскільки в такому разі всі значення будуть дуже малими. 

Як обрати функцію активації

Вибір функції активації залежить від типу задачі, яку потрібно розв’язати: 

1. Східчасту функцію рідко використовують у сучасних нейронних мережах. Можна застосувати на вихідному рівні для бінарної класифікації.

2. Лінійна функція: для задач регресії, де результат може приймати будь-яке значення.

3. ReLu: підходить для прихованих шарів.

4. Leaky ReLu: якщо є проблеми із вмиранням нейронів у ReLU.

5. Сигмоїда: на вихідному шарі для бінарної класифікації та прихованих шарах, коли потрібне перетворення даних на ймовірності.

6. Tanh: замість сигмоїди, коли треба функція активації з нульовим центром і вхідні дані зосереджені навколо нуля.

7. Softmax: підходить для класифікаційних задач.