Функції активації: ступінчаста, лінійна, сигмоїда, ReLU та Tanh

Сьогодні говоримо про функцію активації: як її вибрати та які особливості й недоліки мають різні типи функцій активації — від ступінчастої до гіперболічного тангенсу.

Матеріал великий, тому рекомендуємо зберегти його у закладки на майбутнє. Також для зручності зробили зміст.

ЗМІСТ

Загальна інформація: як працюють нейрони

Функції активації:

1. Порогова (ступінчаста) функція

2. Лінійна функція

3. Сигмоїдна функція (логістична)

4. Гіперболічний тангенс (Tahn)

5. Функція активації ReLU

→ Короткі висновки та порівняльна таблиця

Як працюють нейрони

Нейронна мережа структурно та функціонально повторює роботу нервової системи живих організмів. Вона складається з безлічі штучних нейронів, які пов'язані у вигляді сіток та шарів. Взаємодіючи один з одним, вони передають дані від сітки до сітки та від шару до шару. Завдяки цьому нейронки можуть виконувати складні завдання: наприклад, розпізнавати картинки чи прогнозувати.

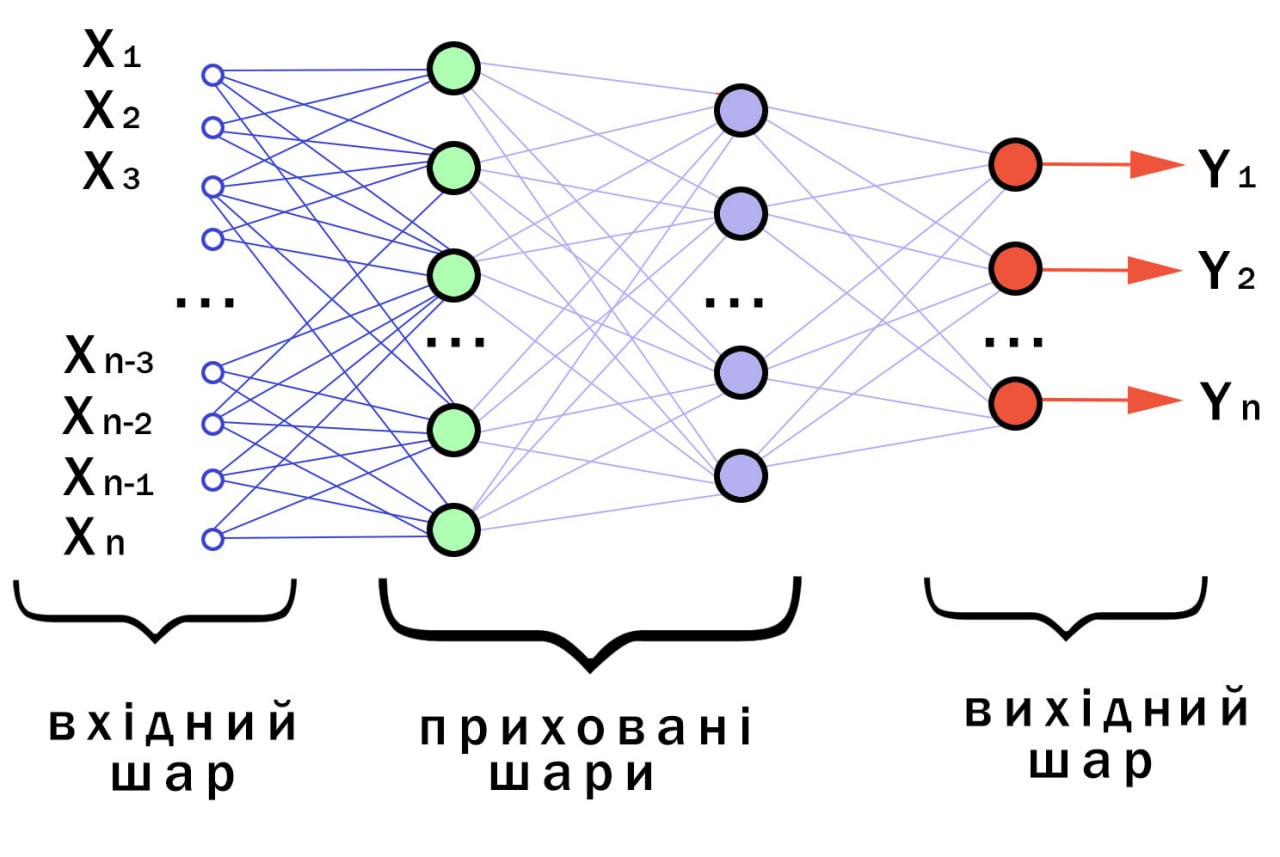
Найпростіша схема нейронної мережі

Базовий блок будь-якої нейронної мережі — це нейрон. Він працює за таким принципом:

1. Штучний нейрон отримує вхідні значення x_i , які можуть виглядати як векторні або числові значення, що представляють ознаки або значення попередніх нейронів.

2. Вхідне значення множиться на відповідну вагу. Ця вага (w_ji) визначає важливість цього входу для обчислень нейрона. Отримані в результаті множення значення підсумовуються:

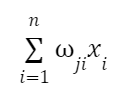
3. До суми зважених значень додається зміщення. Зміщення (bias) у штучному нейроні — це додатковий параметр, деяке константне значення, завдяки якому нейрон може активуватися, навіть якщо зважені входи набувають нульового значення.

Важливо! Без зміщення нейронна мережа могла б представляти лише лінійні відображення, а це обмежило б її здатність розв'язувати складні завдання та витягувати складні патерни з даних.

4. Отримана сума передається через функцію активації, яка застосовує нелінійне перетворення до виваженої суми. Функція активації визначає вихідний сигнал нейрона, додаючи нелінійності до моделі.

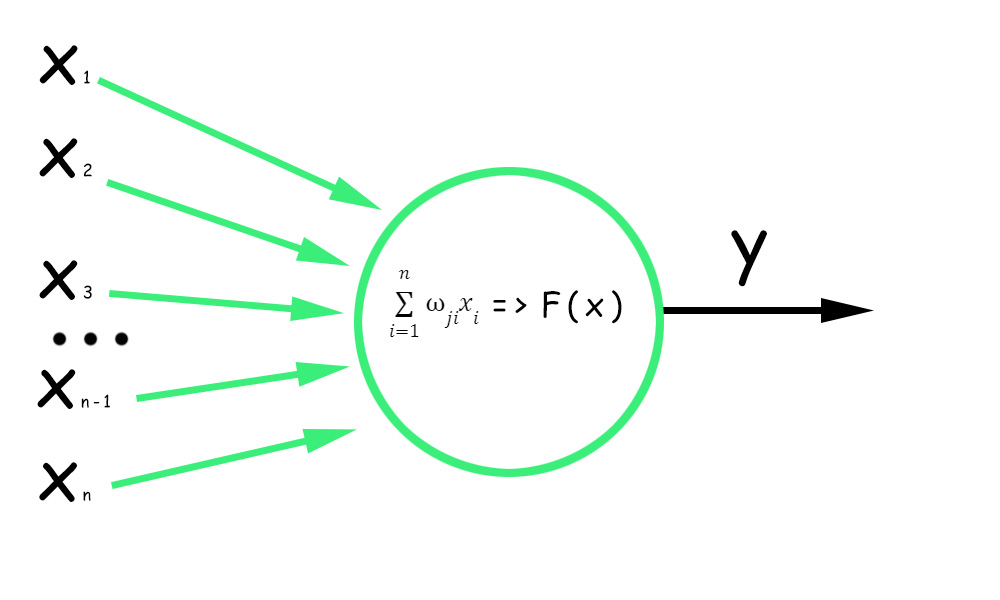
Як працює нейрон

Зверніть увагу, що й усунення, і функція активації разом впливають на активацію нейрона. Зміщення дозволяє встановити базовий рівень активації, тоді як функція активації визначає, як змінюватиметься активація нейрона залежно від входів та зсуву.

У прихованих шарах нейронної мережі зазвичай (не завжди, але найчастіше) використовується та сама функція активації нейронів. Для вихідного шару функція активації трохи змінюється.

Порогова (ступінчаста) функція

Найпростіша функція активації. Іноді її називають функцією Гевісайда. Якщо значення ступінчастої функції перевищує певний поріг, нейрон вважається активованим:

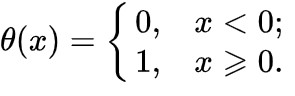
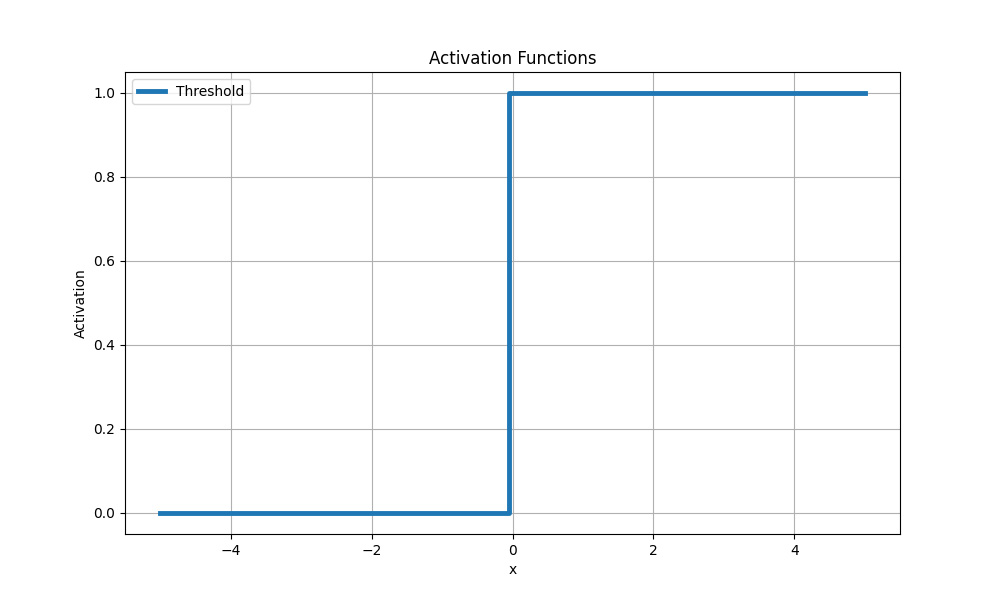
Порогова (ступінчаста) функція активації

Недоліки

Порогова функція безперервна і недиференційована, внаслідок чого ми отримуємо дві проблеми, через які в нейромережах із глибоким навчанням ця функція майже не використовується:

1. Перша проблема пов'язана з алгоритмом зворотного поширення помилки Backpropagation — механізмом навчання нейронної мережі. Завдяки йому налаштовуються ваги зв'язків між нейронами мережі з урахуванням обчислених помилок прогнозування.

Обчислити градієнт, необхідний для оновлення ваг у процесі навчання мережі, можна лише з функціями активації, що диференціюються (градієнт обчислюється за допомогою похідної функції активації з входу нейрона).

2. Друга проблема — стрибки у функції активації Гевісайда. Вони призводять до безперервних змін вихідних значень нейронів за невеликих змін вхідних даних. В результаті мережа може «застрягати» у певних ділянках нейронної мережі, де вихідні значення нейронів стрибають між двома різними значеннями.

Таке застрягання ускладнює відновлення ваг нейронів у цих регіонах, оскільки невеликі зміни ваг не призводять до безперервних змін виходів нейронів. В результаті мережа може не зміститися в потрібному напрямку та не досягти оптимальних значень ваг.

Лінійна функція

Ще одна найпростіша функція активації, в якій зміни вхідного сигналу пропорційно впливають на вихід без будь-яких нелінійних перетворень:

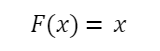
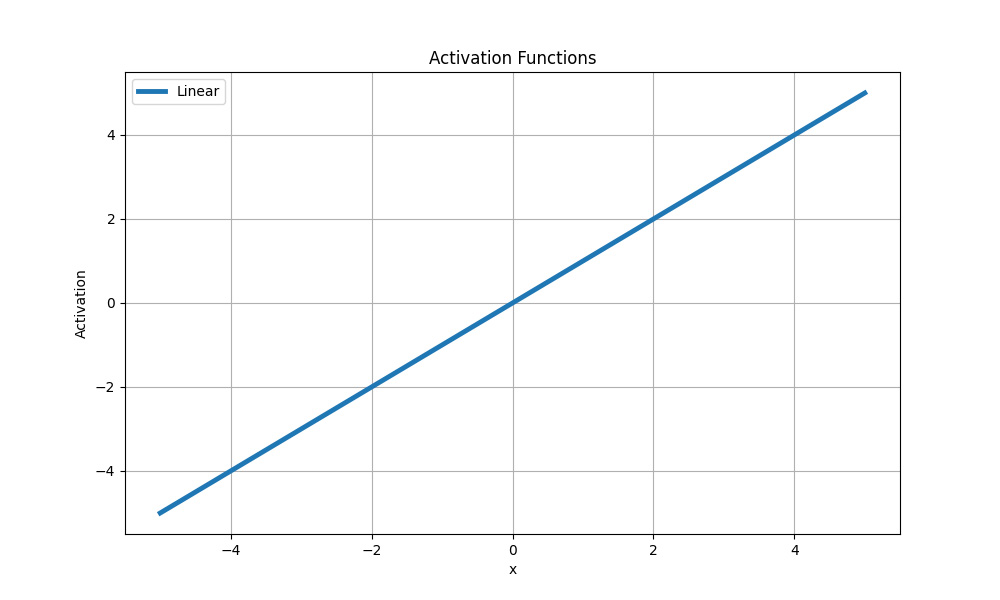
Лінійна функція активації

У зв'язку з цим застосування лінійної функції обмежене завданнями регресії, де потрібне передбачення безперервного значення. Наприклад, у задачі передбачення ціни на нерухомість з урахуванням різних ознак вона може бути застосована до вихідного шару.

Також функція може бути застосована до окремих лінійних шарів мережі, які виконують лінійні операції над входами. У цьому випадку функція активації легко передає значення без нелінійних перетворень.

Приклад використання

Припустімо, ми розв'язуємо завдання прогнозування продажу товарів на основі їхніх рекламних витрат.

Дано:

• відомості про суму грошей, витрачених на рекламу у різних медіаканалах (розкрутка на телебаченні/радіо, у соціальних мережах);
• відповідні відомостям обсяги продажу товарів.

Кінцева мета цієї задачі — побудова моделі, яка прогнозувала б обсяг продажів на основі вхідних даних.

Задіємо нейронну мережу з одним лінійним шаром та лінійною функцією активації. Вхідними даними будуть значення рекламних витрат у різних каналах, а вихідними даними — прогнозований обсяг продажу.

Нейронна мережа з лінійною функцією активації дозволить встановити лінійну залежність між рекламними витратами та обсягом продажу. Модель прагнутиме знайти оптимальні ваги для кожного каналу реклами, щоб якнайкраще передбачати обсяг продажів на основі даних про витрати.

Недоліки

Лінійна функція активації придатна тільки для простих моделей або як заключний шар у нейронній мережі для розв'язання задач регресії, де потрібно виконати прогнозування числового значення.

Сигмоїдна функція (логістична)

Логістична функція нелінійна та стискає вхідні значення від 0 до 1 за формулою:

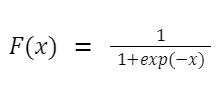
де x — вхідне значення.

Найчастіше сигмоїдна функція активації застосовується у задачах бінарної класифікації, де потрібно передбачити можливість приналежності до одного з двох класів. Вона конвертує вхідні значення у ймовірності, які можуть бути інтерпретовані як імовірність приналежності до позитивного класу.

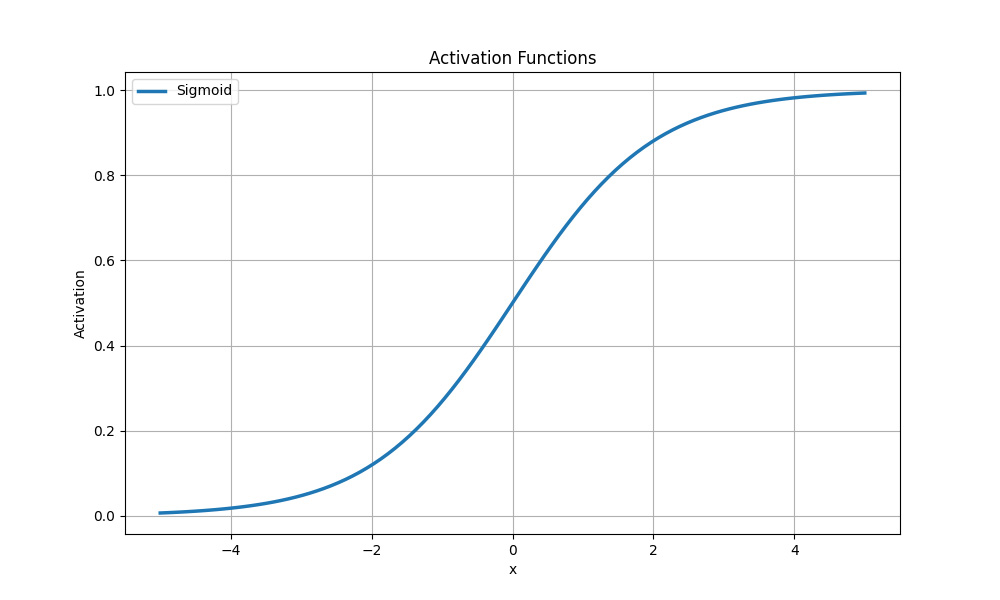
Сигмоїдна функція активації

Приклад використання

Допустімо, є набір даних, що складається з фізичних характеристик пацієнтів. Нам потрібно побудувати модель, яка передбачить, чи є у пацієнта хвороба серця.

Для цього ми можемо використовувати нейронну мережу з одним вихідним нейроном та функцією сигмоїдної активації:

• вхідні дані можуть містити вік пацієнта, рівень холестерину, тиск та інші характеристики;
• вихідний нейрон передбачатиме ймовірність наявності хвороби серця.

Сигмоїдна функція активації перетворює зважену суму вхідних значень та ваг на ймовірність. Наприклад, якщо вихідне значення сигмоїдної функції дорівнює 0.89, це означає, що з імовірністю 89 % модель передбачає наявність проблем із серцево-судинними захворюваннями.

Недоліки логістичної функції

У сфері сильних позитивних чи негативних значень похідна логістичної функції набуває малих значень. Це призводить до появи ефекту згасання градієнта у разі зворотного розповсюдження помилки та замалого його значення, що вкрай неефективно для відновлення ваг нейронів і навчання глибоких нейронних мереж із великою кількістю шарів.

Гіперболічний тангенс (Tahn)

Повна формула гіперболічного тангенсу (tanh) виглядає так:

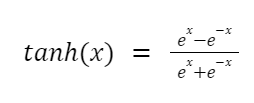
Але оскільки у поведінці тангенс схожий на сигмоїду, її можна уявити так:

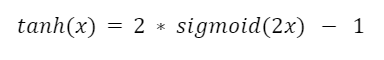
Із сигмоїдою у тангенса є і схожі особливості, і слабкі моменти: вони обидва нелінійні та стискаючі, і обидва обмежені в діапазоні від -1 до 1.

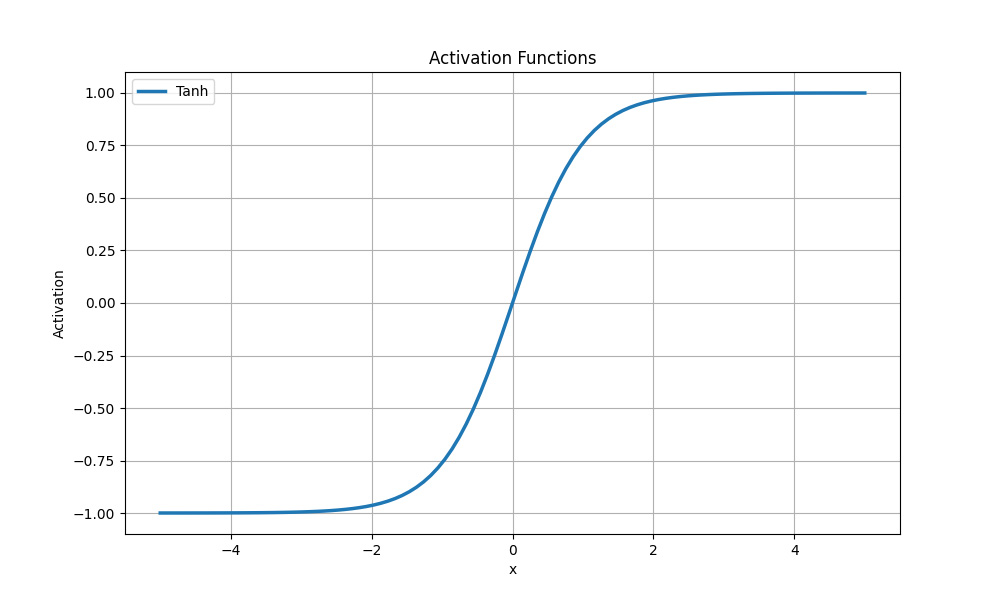
Гіперболічний тангенс

Водночас (порівняно із сигмоїдною функцією активації) tanh(x) має більш помітний градієнт поблизу нуля. Це може бути корисним для моделювання даних, які мають симетричний розподіл навколо нуля та негативні значення яких важливо зберегти.

Недоліки гіперболічного тангенсу

Недоліки tanh(x) також пов’язані з проблемою згасання градієнта.

У процесі використання backpropagation локальний градієнт обчислюється шляхом перемноження похідних функцій активації шарів нейронної мережі. Максимальна похідна гіперболічного тангенсу завжди менше одиниці та обчислюється за формулою:

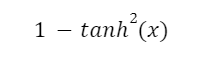
Максимальне значення похідної логістичної функції активації у точці 0 дорівнює ¼ і обчислюється так:

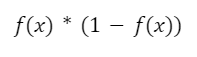
Під час перемноження похідних функцій активації для n шарів максимум локального градієнта буде зменшуватися з кожним шаром і складе 1/(2ⁿ). У разі збільшення числа шарів моделі мережі та відповідного зменшення локального градієнта ваги в ранніх шарах можуть залишатися практично без змін, оскільки градієнт стає дуже малим.

Через згасання градієнта в ранніх шарах оновлення ваги відбуватиметься переважно в глибших шарах, і навчання йтиме з кінця нейронної мережі. В результаті активації сьомого-восьмого шарів ми отримаємо менший внесок у загальний процес навчання порівняно з глибшими шарами, де градієнти зберігаються у вищих значеннях.

Висновок: і логістична функція активації (сигмоїдна), і гіперболічний тангенс часто не рекомендуються для глибоких нейронних мереж, особливо під час використання великої кількості шарів.

Приклад використання гіперболічного тангенсу

Розглянемо завдання з категорії передбачень часових рядів (тимчасовий ряд — це послідовність даних, упорядкованих за часом). Припустімо, є дані про температуру повітря протягом певного періоду часу, і потрібно побудувати модель, яка прогнозуватиме температуру наступного дня.

Ми застосовуємо рекурентну нейронну мережу (RNN), де як функцію активації взято tanh(x). У RNN є пам'ять, яка дозволяє їй враховувати попередні значення та передбачати майбутні значення на основі цієї історії.

Код на Python із використанням фреймворку TensorFlow виглядатиме приблизно так:

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, LSTM
# Підготовка тимчасового ряду для аналізу
# ...
# Передобробка даних
# ...
# Створення  моделі
model = Sequential()
model.add(LSTM(32, activation='tanh', input_shape=(time_steps, input_dim)))
model.add(Dense(1))
# Компіляція 
model.compile(loss='mean_squared_error', optimizer='adam')
# Навчання моделі
model.fit(X_train, y_train, epochs=10, batch_size=32)
# Прогнозування
predictions = model.predict(X_test)

Важливо! У цьому коді передбачається, що дані вже оптимізовані та готові до використання.

Загальний принцип побудови нейронної мережі такий:

• За допомогою класу Sequential() створюється послідовна модель нейронної мережі.
• Метод model.add() додає шар LSTM (з 32 прихованими нейронами та функцією активації гіперболічного тангенсу).
• Параметром input_shape=(time_steps, input_dim) визначаємо вхідний розмір моделі, де time_steps — кількість тимчасових кроків, а input_dim — кількість ознак на кожному тимчасовому кроці.
• Через команду model.compile() компілюється модель. В ній вказується функція втрат mean_squared_error (середньоквадратична помилка) і оптимізатор adam, який використовується для оновлення ваг моделі.
• Через метод навчання model.fit() виконуємо тренування моделі на навчальних даних (X_train, y_train).
• Вказуємо кількість епох epochs=10 (визначає, скільки разів весь набір навчальних даних проходитиме через нейронну мережу в процесі навчання) та розмір пакета даних, що використовуються для кожного оновлення вагових коефіцієнтів, — batch_size=32.
• Після завершення процедури навчання застосовуємо model.predict() до тестових даних (X_test) для отримання передбачених значень.

Функція активації ReLU

ReLU (Rectified Linear Unit) — одна з найпопулярніших функцій активації, що використовуються як у мережах з низьким числом шарів, так і в моделях deep learning.

Формула ReLU:

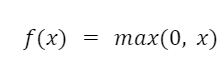
де x — вхідний сигнал, а f(x) — вихідний.

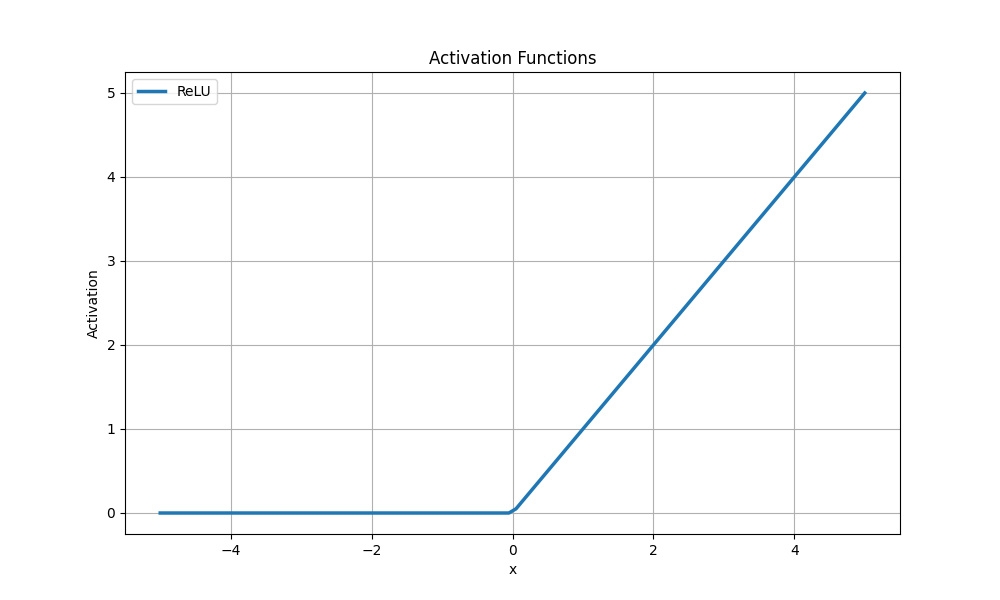
Функція активації ReLU

Ця функція активації (як і наявні її модифікації) усуває проблеми зі зникаючим градієнтом. Градієнти для значень більше нуля залишаються ненульовими, що забезпечує ефективне поширення градієнтів та оновлення ваги в процесі тренування.

Корисно знати! Модифіковані функції Leaky ReLU, Parametric ReLU (PReLU) і Exponential Linear Unit (ELU) також мають властивості, які сприяють запобіганню згасання градієнта. Наприклад, Leaky ReLU додає невеликий нахил для негативних значень, а ELU має експоненційну залежність негативних значень.

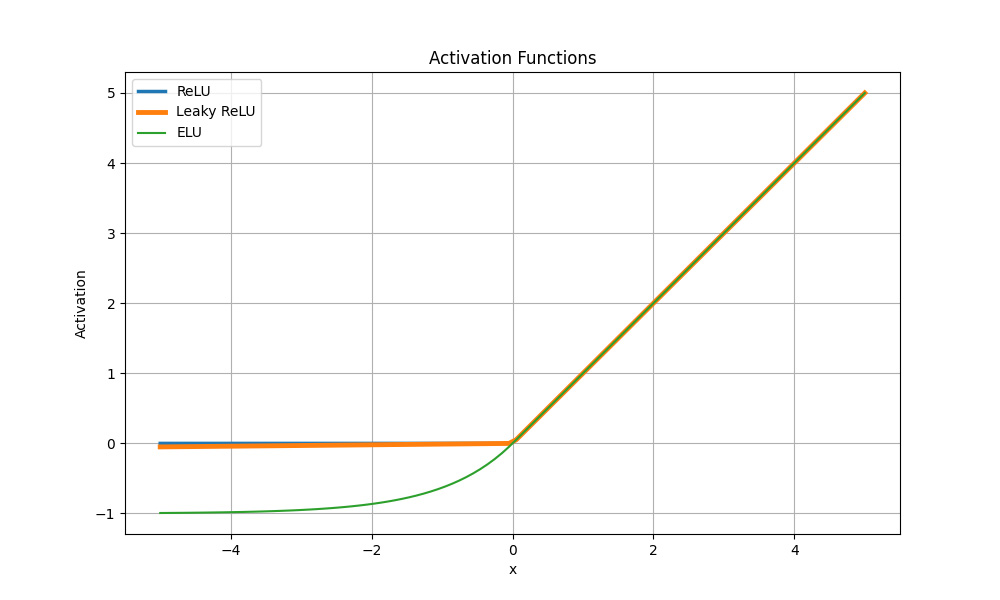
Порівняння функції активації ReLU з її модифікаціями

Хоча на графіку помітна її часткова лінійність, функція ReLU нелінійна та комбінації з нею також нелінійні.

Функція універсальна і придатна для будь-яких завдань, не вимагаючи великих обчислювальних потужностей. Усі негативні значення функція заміняє на нуль і передає позитивні значення без змін. Градієнти для позитивних значень залишаються ненульовими, що дозволяє ефективно розповсюджувати градієнти та оновлювати ваги під час навчання.

Функція ReLU активує лише окремі нейрони, залишаючи інші неактивними. Завдяки цьому мережа може навчатися на більш розріджених уявленнях даних — і знижується ризик перенавчання.

Недоліки функції ReLU

Очевидний мінус функції активації ReLU — її ненормалізованість. Так само як і у сигмоїдної функції активації, вихідне значення ReLU завжди знаходиться в інтервалі від 0 до ∞, що може бути обмежувальним у деяких випадках.

Як розв'язати проблему: нормалізувати дані перед застосуванням функції активації ReLU.

Через великі значення ваги або незбалансованість даних у ReLU (немодифікованих версіях) може проявлятися проблема «мертвих нейронів», що знижує продуктивність у моделях deep learning. Це означає, що якщо ваги для певних вхідних даних є негативними або близькими до нуля, то функція ReLU активуватиме нейрон тільки для позитивних значень входу, а інші залишаться пасивними.

Висновок

Функція активації визначає вихідний сигнал нейрона з урахуванням його входу. Ми просто підставляємо до неї підсумоване значення добутку нейронних вхідних сигналів та коефіцієнтів ваг — і отримуємо вихідний сигнал нейронної мережі.

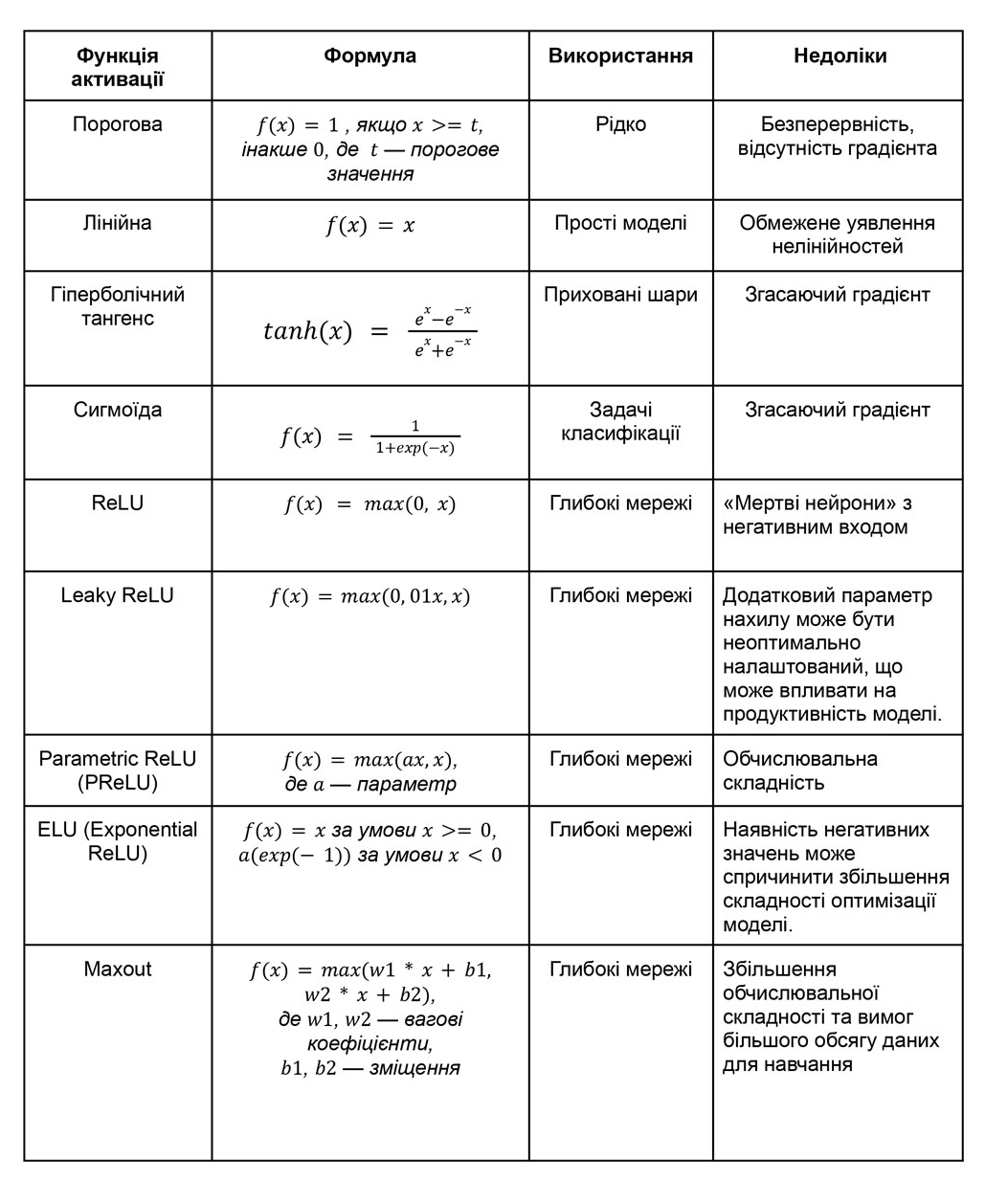
Нижче вказані переваги та недоліки різних функцій активації:

• Порогова функція бінарна та використовується рідко через свою безперервність і відсутність градієнта.
• Лінійна функція активації передає вхідний сигнал без змін, тому застосовується у простих моделях і не підходить для представлення складних нелінійних залежностей.
• Гіперболічний тангенс (tanh) стискає вхідні значення в діапазоні від -1 до 1. Він часто використовується вприхованих шарах нейронних мереж зберігаючи негативні значення та забезпечуючи нелінійність.
• Сигмоїда перетворює вхідні значення в діапазоні від нуля до одиниці. Вона часто використовується в задачах класифікації, але страждає від проблеми градієнта, що згасає, під час навчання глибоких нейронних мереж.
• Функція активації ReLU (Rectified Linear Unit) активує нейрон, якщо вхід позитивний, інакше — виходить 0. Вона широко застосовується у глибоких нейронних мережах завдяки простоті та відсутності згасаючого градієнта, але може викликати «мертві нейрони» з негативним входом.

Наостанок — таблиця з порівнянням основних функцій активації та деяких модифікацій ReLU. Зберігайте собі, щоби була під рукою: