Криптографічні провали PlayStation, SaltStack та Hyundai: Як помилки інженерів призводять до вразливості систем
3 приклади з життя розбирає Руслан Кіянчук
Бажання захистити інформацію від сторонніх очей виникло в людей, щойно вони навчилися писати. Відтоді криптографія пройшла довгий шлях розвитку, проте лише в середині XX ст. ми отримали достатньо теоретичного підґрунтя для створення надійних методів шифрування. Сучасні криптографічні алгоритми настільки складні в обчисленні, що дешифрування інформації без доступу до ключа на практиці є неможливим.
Однак інформаційні системи досі часто страждають від вразливостей, але тепер вони виникають не через слабкі криптоалгоритми, а через їхнє неправильне застосування.

Про те, як нерозуміння принципів роботи криптографічних алгоритмів з боку розробників призводить до повної компрометації захисту системи, розповідає інженер з криптографії та розробки програмного забезпечення в NAVAN Руслан Кіянчук. За його плечима — понад 10 років роботи в ІТ-індустрії Кремнієвої долини, участь у розробці блокового симетричного шифру, який став національним стандартом шифрування України, розробка систем автентифікації у FinTech-компаніях та створення авторського курсу «Основи криптографії» для студентів robot_dreams.
SaltStack та шифрування RSA, що не працює
Коректна та безпечна реалізація алгоритму RSA є нетривіальним завданням навіть для фахівців, оскільки вимагає глибокого розуміння не лише його математичного апарату, криптографії, моделі загроз, а й архітектури процесорів та програмної інженерії. Проте для застосування вже готової реалізації RSA достатньо загального розуміння принципів роботи алгоритму.
Основні параметри RSA складаються з відкритої експоненти e, секретної експоненти d та модуля N, підібраних таким чином, що
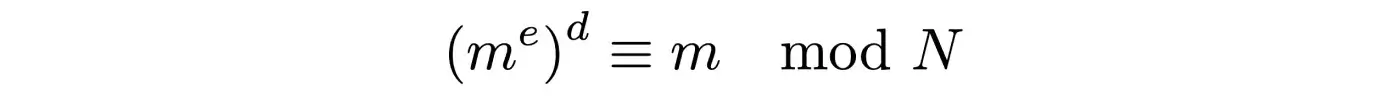
Тому для зашифрування ми використовуємо відкриту експоненту отримувача: беремо наше повідомлення в бінарному представленні, підносимо його до степеня e та зводимо до модуля N (тобто беремо залишок від ділення отриманого числа на N):
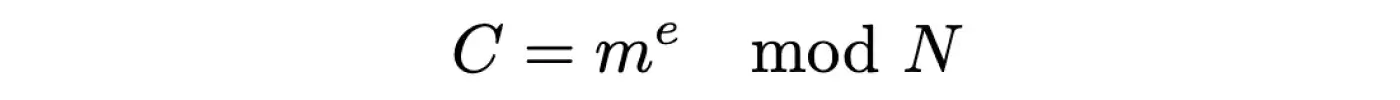
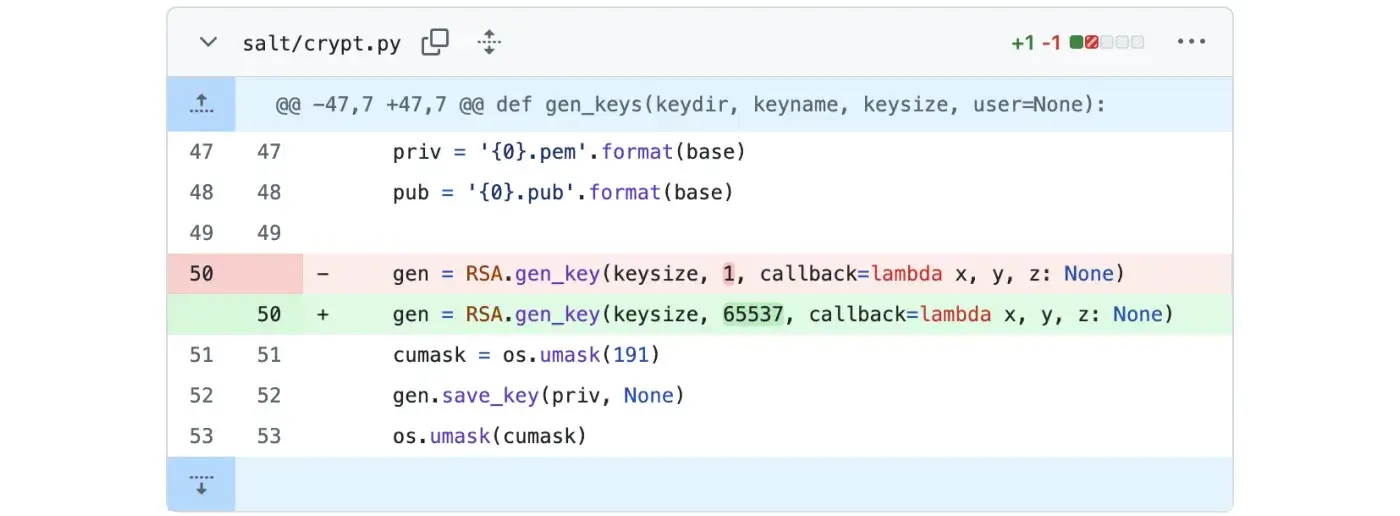
Проєкт для керування конфігурацією Salt застосовував RSA для захисту повідомлень, але під час генерування параметрів криптосистеми через нерозуміння нюансів роботи алгоритму обрали значенням відкритої експоненти 1.
На жаль, криптографічна бібліотека, якою користувалися в проєкті, прийняла такі параметри та не видала жодної помилки. Проте, знаючи принцип роботи RSA, достатньо шкільної арифметики, щоб зрозуміти, в чому проблема такого значення: піднесення до степеня 1 не змінює число, m1 = m, тож повідомлення залишається незмінним.
Згодом цю помилку помітили під час аудиту коду фахівцем з кібербезпеки та виправили на рекомендоване значення відкритої експоненти: 65537 (або 216+1).
Hyundai списав домашку й забув підставити свої значення
У 2022 році один розробник хотів модифікувати програмне забезпечення мультимедійної системи свого авто Hyundai, проте модифікація й оновлення ПЗ були захищені шифруванням та електронними цифровими підписами. Досліджуючи доступні сирці мультимедійної системи та використовуючи метод спроб і помилок, він з’ясував, що ключ, яким шифрували прошивку, був не випадковим, а взятим з прикладів стандарту NIST SP 800-38A від Національного інституту стандартів і технологій США.
Надихнувшись таким недолугим захистом, інженер продовжив копирсатися в бінарних файлах оновлювача ПЗ і згодом зрозумів, що RSA-ключ для підпису оновлень також взяли з онлайн-статті — прикладу застосування алгоритму RSA.
Компрометація PlayStation 3 через хибу в ECDSA
Для захисту програмного забезпечення в PlayStation 3 використовували алгоритм ECDSA. Це гарантувало, що на PS3 можна запустити лише програмне забезпечення з електронним цифровим підписом від Sony.
Операції в алгоритмі ECDSA здійснюються в групі точок еліптичної кривої, проте нам необовʼязково розбиратися з додаванням точок на еліптичній кривій, щоб розуміти загальний принцип його дії, — ми можемо сприймати операції алгоритму як звичайні арифметичні операції над змінними. Головне памʼятати, що «під капотом» — точки на кривій, які мають координати x та y.
Еліптична крива secp256k1
ECDSA має кілька загальних параметрів, що є загальнодоступними:
- Рівняння кривої. Одна зі стандартних еліптичних кривих для ECDSA — це secp256k1 і має рівняння:
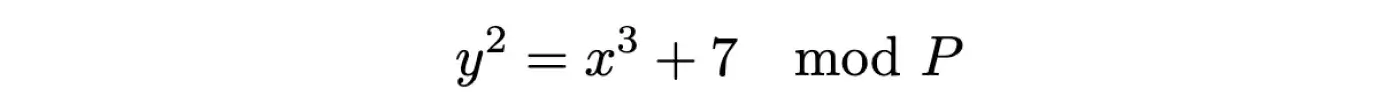
де модуль P = 2256 - 232 - 29 - 28 - 27 - 26 - 24 - 1.
- G — це «генератор» групи точок еліптичної кривої (базова точка, з якої ми починаємо відлік).
- n — порядок групи, тобто розмір множини всіх точок (оскільки всі операції ми виконуємо за модулем, то кількість точок кривої скінченна, хоч і дуже велика).
Потім генерують ключі:
1. Обирають випадкове число d в інтервалі 1..n. Це стає секретним ключем. У нашому випадку Sony згенерувало такий ключ для підпису оновлень.
2. Відкритий ключ Q = d · G.
Тоді для створення підпису виконують такий алгоритм:
1. Повідомлення, яке потрібно підписати, хешують за допомогою SHA-256:
h = H(M)
2. Обирають випадкове число k в інтервалі 1..n.
3. Генерують точку R = k · G. Потім ми зберігаємо лише координату x цієї точки: r = R.x
4. Генерується доказ підпису:
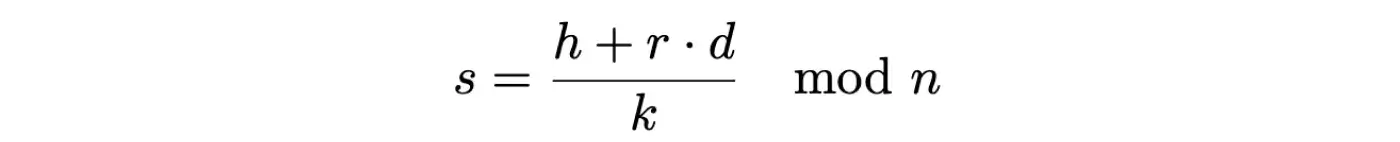
Значення {r, s} є цифровим підписом.
Проте, якщо керуватися лише цим описом і не вивчати алгоритм глибше, можна припуститися фатальної помилки в його реалізації. Випадкове значення k є рандомізатором підпису, і тому воно має бути не лише випадкове, а й унікальне для кожного окремого підпису. Саме на випадковості цього числа ґрунтується складність підробки підпису.
На жаль, Sony не взяли до уваги цей нюанс, а тому для підпису оновлень прошивки PlayStation 3 просто одноразово згенерували випадкове k та використовували одне й те саме його значення в кожному підписі. А в такому разі достатньо мати всього 2 згенерованих підписи, щоб повністю відновити секретний ключ, яким їх зроблено.
Згадаємо: якщо у нас є два підписи, створені одним секретним ключем, то ми маємо два значення s1 та s2:
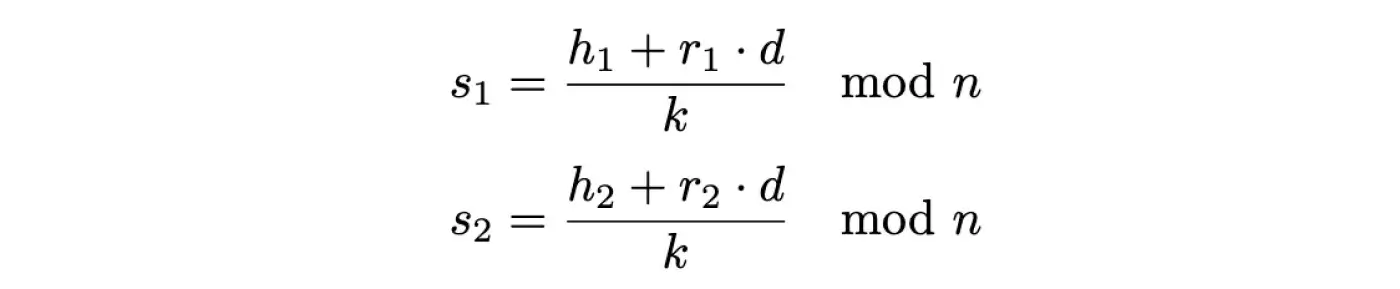
Нам відомі значення s1, s2, r1, r2, n, проте невідомі d та k. Розгляньмо різницю s1 та s2:
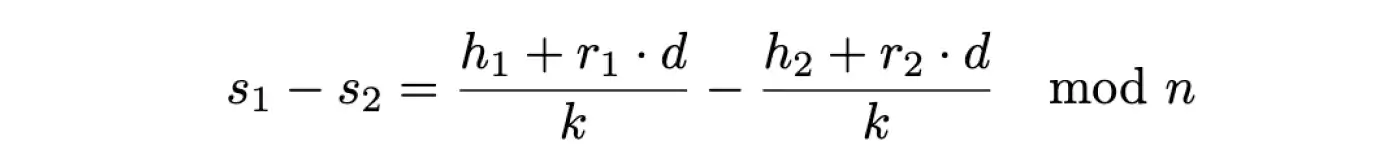
Бачимо, що в цьому разі доданки, які містять невідоме d, можна скоротити:
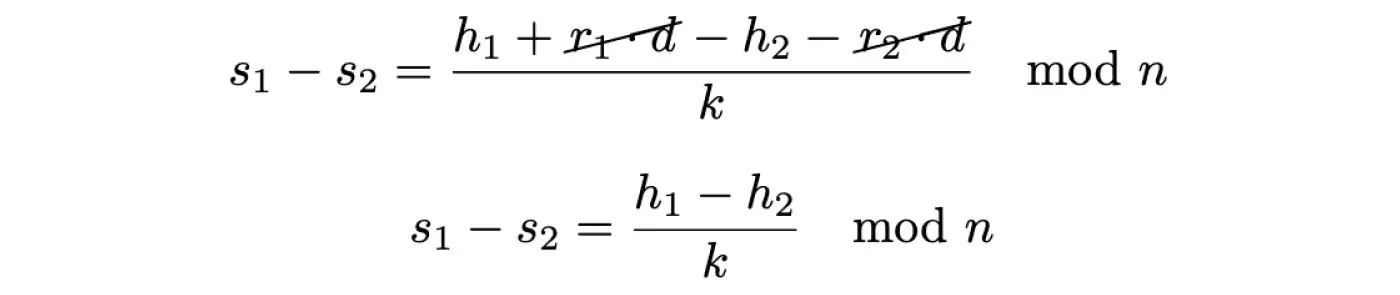
Тепер рівняння містить лише одну невідому змінну k, а отже, можемо розв’язати рівняння для неї та віднайти невідому:
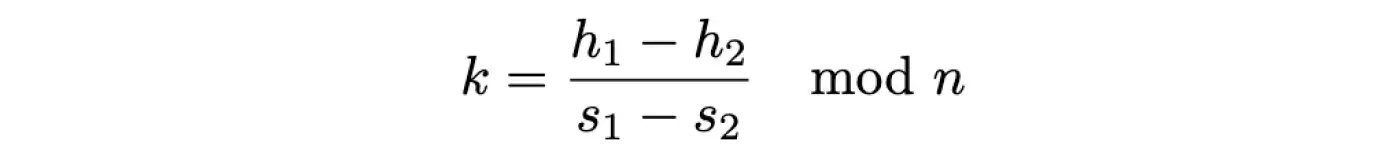
Знаючи k, можемо повернутися до нашого рівняння доказу підпису (будь-якого з двох, але для прикладу оберемо перший):
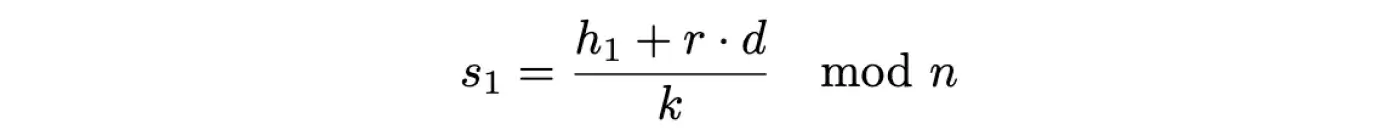
Тепер нам невідома лише d (секретний ключ), тому можемо розв’язати рівняння для цієї змінної. Позбудемося дробу, домноживши обидві частини рівняння на k:
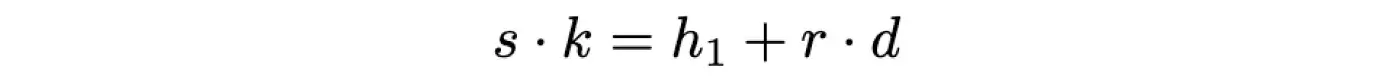
Перенесемо доданок з невідомою ліворуч:
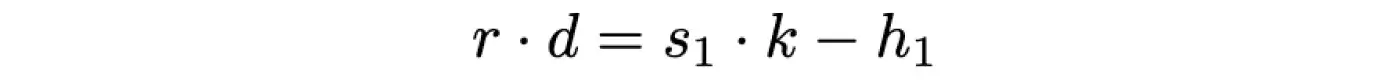
Тоді маємо:
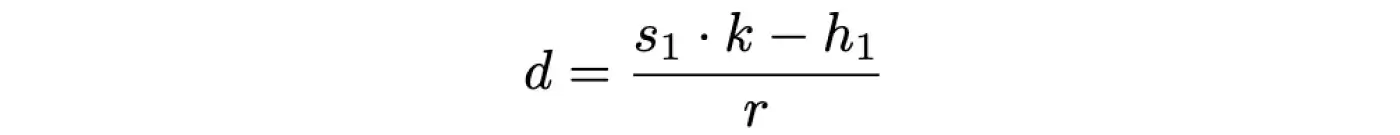
А отже, тепер ми знаємо секретний ключ, яким створено підписи, й можемо генерувати нові.
Варто зазначити, що використання статичного значення k призводить до того, що всі підписи мають одне й те саме значення r. Це й помітили хакери групи fail0verflow у 2010 році та, застосовуючи описаний вище механізм, змогли відновити секретний ключ Sony, чим отримали повний доступ до встановлення будь-якого програмного забезпечення на PlayStation 3.
Підсумок
Як бачимо з наведених прикладів, навіть інженери найвідоміших технологічних компаній світу продовжують регулярно припускатися помилок, що компрометує захист систем та призводить до вразливостей. Ми дедалі більше покладаємося на технології у повсякденному житті, і майже кожен сучасний пристрій має канали звʼязку та потребує їхнього надійного захисту. А отже, розуміння основ криптографії є вкрай важливим для кожного розробника.



