Полный гайд по алгоритмам сортировки на Java для новичков ч.1
Часть 1. Сортируем вставкой, выбором, пузырьком и не только
В этой статье разбираем алгоритмы сортировки Java и примеры их реализации. В том числе выясняем, что такое алгоритмы сортировки, зачем они нужны и как выбрать подходящий алгоритм для конкретной задачи.
Что такое алгоритм сортировки
Алгоритм сортировки — это набор инструкций, который принимает на входе алгоритм или список и упорядочивает его элементы в указанном порядке
Сортировка обычно проводится в числовом или алфавитном порядке, по возрастанию (0–9 / А–Я) или по убыванию (9–0 / Я–А).
Вот как это выглядит:
- Неотсортированный массив:
а л г о р и т м - Сортировка массива по возрастанию:
а г и л м о р т - Сортировка массива по убыванию:
т р о м л и г а
Зачем нужны алгоритмы сортировки и какими они бывают
Алгоритмы — это инструкции для оптимального решения проблем. Конкретно у алгоритмов сортировки есть разные практические применения. Например, они упрощают работу с поиском, базами и структурами данных.
Алгоритмы сортировки разделяют на категории по нескольким факторам:
- Количество требуемых перестановок или инверсий.
- Количество сравнений.
- Наличие рекурсии.
- Стабильность (элементы с одним и тем же значением будут расположены в отсортированном массиве в том же порядке относительно друг друга, что и в исходном).
- Объем дополнительной памяти. Дополнительная память — это память помимо памяти для входных данных. Она используется для хранения промежуточных данных и выражается в величинах от O(1) до O(n)).
Как выбрать подходящий алгоритм сортировки
Чтобы выбрать алгоритм сортировки, нужно задать себе несколько вопросов:
- Какой размер сортируемой структуры данных?
- Сколько памяти доступно?
- Нужно ли расширять структуру?
То есть вам нужно определить требования и рассмотреть ограничения используемой системы.
Распространенные алгоритмы сортировки
Ниже рассмотрим распространенные методы сортировки массива на Java для разной временной сложности.
Временная сложность показывает, насколько влияет количество входных данных на время выполнения алгоритма.
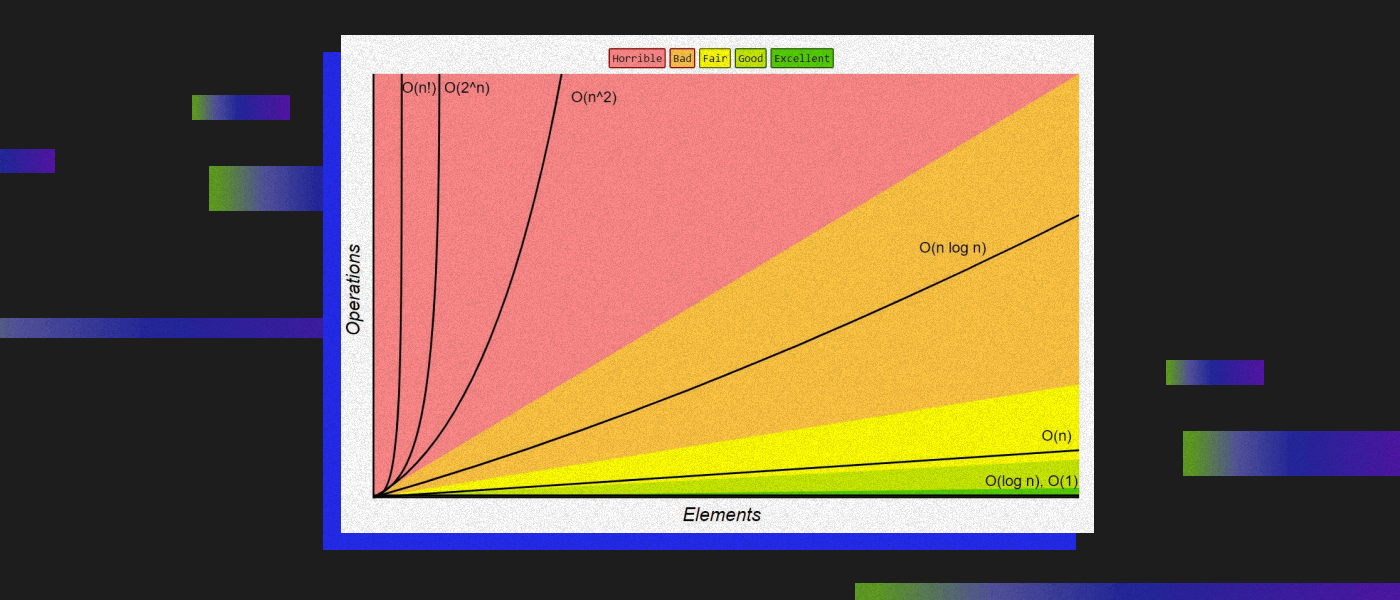
Источник: Big-O Complexity Chart
O(n2):
- сортировка вставкой Java;
- сортировка выбором Java;
- сортировка пузырьком Java.
O(n log n):
- сортировка слиянием Java;
- пирамидальная сортировка Java;
- быстрая сортировка Java;
- сортировка Шелла на Java.
O(n+K):
- сортировка подсчетом Java.
Также существует сортировка перестановкой, при которой алгоритм последовательно генерирует перестановки входных данных, пока не найдет отсортированную. Это самый неэффективный алгоритм, который только можно себе представить. Его временная сложность в наихудшем случае составляет O(∞), так как этот алгоритм не имеет верхнего предела, поэтому разбирать подробно мы его не будем.
Ниже разбираем первую часть этого списка ↓
Сортировка вставкой Java
Сортировка вставкой — это простой алгоритм сортировки для массивов с небольшим количеством элементов.
Массив виртуально разделяется на отсортированную и неотсортированную части. Затем элементы из отсортированной части перемещаются на необходимую позицию в отсортированной части.
Алгоритм сортировки вставкой Java
Чтобы отсортировать массив размером N по возрастанию методом вставки, нужно провести итерацию по массиву и сравнить текущий элемент (ключ) с предшествующим. Если ключевой элемент меньше предшественника, то сравнить его с элементами, расположенными перед предшественником. Переместить большие элементы на одну позицию вверх, чтобы создать место для переставляемого элемента.
Пример: сортировка вставкой Java
Примечание. Все методы сортировки массива в этой статье помещены в пакет sorting и наследуют интерфейс SortingMethod, который определен в отдельном классе. Код класса SortingMethod и класса, который демонстрирует результаты работы методов, вы найдете в конце статьи.
package sorting;
// Java class implementing Insertion Sort
public class InsertionSort implements SortingMethod {
// Sorts an array
public void sort(int array[]){
// Iterate through elements
for ( int i = 1; i < array.length; i++){
// Assign the key
int key = array[i];
int j = i - 1;
// Place the element before all greater elements
while (j >= 0 && array[j] > key){
array[j+1] = array[j];
j--;
}
array[j+1] = key;
}
}
}
Характеристики сортировки вставкой
Временная сложность: O(n2)
Дополнительное пространство: O(1)
Эффективна для малых значений данных. Является адаптивной, то есть подходит также для наборов данных, которые уже частично отсортированы.
Сортировка выбором Java
Сортировка выбором — это простой и эффективный алгоритм сортировки, который на каждой итерации выбирает самый маленький (или больший) элемент из неотсортированной части массива/списка и перемещает его в отсортированную.
Алгоритм сортировки выбором Java
Чтобы отсортировать массив методом сортировки выбором, нужно итеративно выбирать наименьший или наибольший элемент из неотсортированного подмассива и менять его местами с первым элементом из неотсортированного подмассива. Повторять этот процесс для каждого элемента из неотсортированного подмассива, пока не будет отсортирован весь массив.
Пример: сортировка выбором Java
package sorting;
// Java class implementing Insertion Sort
public class SelectionSort implements SortingMethod {
// Sorts an array
public void sort(int array[]){
int len = array.length;
// Iterate through elements
for ( int i = 0; i < len - 1; i++){
// Find the smallest element in the unsorted part
int i_smallest = i;
for (int j = i+1; j < len; j++){
if (array[j] < array[i_smallest])
i_smallest = j;
}
/* Swap the smallest element with the first element
of the unsorted subarray*/
int tmp = array[i_smallest];
array[i_smallest] = array[i];
array[i] = tmp;
}
}
}
Характеристики сортировки выбором
Временная сложность: O(n2), потому что используется два цикла:
- для выбора элементов из массива по одному = O(n);
- для сравнения выбранного элемента с каждым остальным элементом массива = O(n);
- совокупная сложность = O(n) * O(n) = O(n*n) = O(n2).
Дополнительное пространство: O(1), потому что дополнительная память используется только для хранения одного значения при перестановке.
Сортировка выбором делает не более O(n) перестановок и будет полезной, когда запись в память обходится дорого.
Сортировка пузырьком Java
Сортировка пузырьком — это простейший алгоритм сортировки, которая осуществляется путем повторяющейся перестановки смежных элементов, если они расположены не в требуемом порядке.
Этот алгоритм не подходит для крупных наборов данных, потому что его сложность в среднем и сложность в худшем случае довольно высока.
Алгоритм сортировки пузырьком Java
Провести итерацию слева, сравнивая соседние элементы и помещая больший из них справа. В результате сначала будет найден наибольший элемент, который затем будет перемещен в крайнюю правую позицию.
Повторить процесс для левого подмассива, который еще не отсортирован: найти в нем наибольший элемент и поместить его в крайнюю правую позицию подмассива. Повторять процесс, пока не будут отсортированы все данные.
Пример: пузырьковая сортировка Java
package sorting;
// Java class implementing Bubble Sort (optimized)
public class BubbleSort implements SortingMethod {
public void sort(int array[])
{
int tmp, length = array.length;
boolean swapped;
for (int i = 0; i < length - 1; i++) {
swapped = false;
for (int j = 0; j < length - i - 1; j++) {
if (array[j] > array[j + 1]) {
// Swap left and right
tmp = array[j];
array[j] = array[j + 1];
array[j + 1] = tmp;
swapped = true;
}
}
// If no two elements were swapped,
// exit loop
if (swapped == false)
break;
}
}
}
Характеристики сортировки пузырьком
Временная сложность: O(n2)
Дополнительное пространство: O(1)
Пузырьковая сортировка проста для понимания, и ее несложно реализовать. Для нее не требуется дополнительное пространство, кроме временных переменных. Это стабильный алгоритм сортировки, то есть элементы с одним и тем же значением будут расположены в том же порядке относительно друг друга и в отсортированном массиве.
В то же время сортировка пузырьком очень медленно обрабатывает крупные наборы данных, потому что ее временная сложность равна O(n2). Кроме того, этот алгоритм основан на сравнении, что в определенных случаях может ограничивать его эффективность.
Сортировка слиянием Java
Сортировка слиянием — это алгоритм сортировки, который делит массив на подмассивы, сортирует каждый из них, а затем объединяет отсортированные подмассивы, что в результате дает отсортированный массив.
Алгоритм сортировки слиянием Java
Рекурсивно разделять массив на половины, пока его возможно делить. В результате в каждом подмассиве остается только один элемент, а такой массив всегда отсортирован. Объединить отсортированные подмассивы в один отсортированный массив.
Пример: сортировка слиянием Java
package sorting;
// Java class implementing Merge Sort
public class MergeSort implements SortingMethod {
// Merges two subarrays of array[].
// First is from leftIndex to midIndex
// Second is from midIndex+1 to rightIndex
void merge(int array[], int leftIndex, int midIndex, int rightIndex)
{
// Find sizes of subarrays
int leftLength = midIndex - leftIndex + 1;
int rightLength = rightIndex - midIndex;
// Create temporary arrays
int leftArray[] = new int[leftLength];
int rightArray[] = new int[rightLength];
// Copy data to temp arrays to process
for (int i = 0; i < leftLength; ++i)
leftArray[i] = array[leftIndex + i];
for (int j = 0; j < rightLength; ++j)
rightArray[j] = array[midIndex + 1 + j];
// Merge temporary arrays
// Initial indices of first and second subarrays
int i = 0, j = 0;
// Initial index of array
int k = leftIndex;
// Traverse arrays choosing elements in order
while (i < leftLength && j < rightLength) {
if (leftArray[i] <= rightArray[j]) {
array[k] = leftArray[i];
i++;
}
else {
array[k] = rightArray[j];
j++;
}
k++;
}
// Copy remaining elements from leftArray and rightArray
while (i < leftLength) {
array[k] = leftArray[i];
i++;
k++;
}
while (j < rightLength) {
array[k] = rightArray[j];
j++;
k++;
}
}
// Sorts array[leftIndex..rightIndex] using merge()
public void mergeSort(int array[], int leftIndex, int rightIndex)
{
if (leftIndex < rightIndex) {
// Find the middle index
int midIndex = leftIndex + (rightIndex - leftIndex) / 2;
// Sort first and second subarrays
mergeSort(array, leftIndex, midIndex);
mergeSort(array, midIndex + 1, rightIndex);
// Merge the sorted subarrays
merge(array, leftIndex, midIndex, rightIndex);
}
}
public void sort(int array[])
{
mergeSort(array, 0, array.length -1);
}
}
Характеристики сортировки слиянием
Временная сложность: O(N log(N))
Дополнительное пространство: O(N)
Сортировка слиянием применяется в следующих целях:
- сортировка крупных наборов данных — благодаря тому, что гарантированная сложность в худшем случае равна O(n log n);
- внешняя сортировка — когда набор данных для сортировки слишком велик и не помещается в память;
- пользовательская сортировка — сортировку слиянием можно адаптировать для различных случаев распределения входных данных, например, для частично отсортированных, почти отсортированных или полностью несортированных данных;
- подсчет количества инверсий.
Пирамидальная сортировка Java
Пирамидальная сортировка — это метод сортировки на основе сравнения, который использует структуру данных двоичной кучи.
Эта сортировка напоминает сортировку выбором. Сначала определяется минимальный элемент и помещается в начало. Тот же процесс повторяется для остальных элементов.
Алгоритм пирамидальной сортировки Java
- создать кучу из заданного входного массива;
- повторять следующие шаги, пока размер кучи не станет равным единице:
- • поменять местами корневой элемент кучи (который является самым большим элементом) с последним элементом кучи;
- • удалить последний элемент кучи (который теперь находится на правильной позиции);
- • поднять оставшиеся элементы кучи.
- отсортированный массив создается путем изменения порядка элементов во входном массиве.
Пример: пирамидальная сортировка Java
package sorting;
// Java class implementing Heap Sort
public class HeapSort implements SortingMethod {
// Sorts using heap sort
public void sort(int array[])
{
int length = array.length;
// Build heap
for (int i = length / 2 - 1; i >= 0; i--)
heapify(array, length, i);
// Extract elements from heap one by one
for (int i = length - 1; i > 0; i--) {
// Move current root to the final position
int tmp = array[0];
array[0] = array[i];
array[i] = tmp;
// Call heapify for the reduced heap
heapify(array, i, 0);
}
}
// Makes a heap
void heapify(int array[], int length, int i)
{
int greatest = i;
int l = 2 * i + 1;
int r = 2 * i + 2;
// If left child is greater than the root
if (l < length && array[l] > array[greatest])
greatest = l;
// If right child is greater than the greatest
if (r < length && array[r] > array[greatest])
greatest = r;
// If the greatest is not root
if (greatest != i) {
int tmp = array[i];
array[i] = array[greatest];
array[greatest] = tmp;
// Recursively heapify the sub-tree
heapify(array, length, greatest);
}
}
}
Характеристики пирамидальной сортировки
Временная сложность: O(n log n)
Дополнительное пространство: O(1)
Пирамидальная сортировка выполняется «на месте». Ее типовая реализация нестабильна, но ее можно сделать такой. Она примерно в 2–3 раза медленнее быстрой.
Для пирамидальной сортировки используется минимальный объем памяти. Она проста для понимания, поскольку в ней не используются продвинутые концепции, например, рекурсия. При этом пирамидальная сортировка нестабильна, поскольку порядок элементов относительно друг друга может измениться. Кроме того, она не совсем эффективна для обработки очень сложных данных.
Код для демонстрации времени сортировки
Создайте папку sorting и поместите в нее файлы с кодом всех приведенных выше классов (например, код класса MergeSort — в файл MergeSort.java и так далее).
Создайте в этой же папке файл SortingMethod.java с таким кодом:
package sorting;
// Java class declaring SortingMethod interface
interface SortingMethod {
// Sorts an array
public void sort(int array[]);
}
В той же папке создайте файл SortingDemo.java с таким кодом:
package sorting;
// Java class demonstrating different sorting methods
public class SortingDemo {
// Prints an array
static void printArray(int array[])
{
int n = array.length;
for (int i = 0; i < n; ++i)
System.out.print(array[i] + " ");
System.out.println();
}
// Main method
public static void main(String args[])
{
System.out.println();
System.out.println("* Array sorting demo *");
System.out.println();
// Declare the array of sorting method instances
SortingMethod sortingMethods[] = {
new InsertionSort(),
new SelectionSort(),
new BubbleSort(),
new MergeSort() ,
new HeapSort(),
new BogoSort()
};
// Demonstrate that methods work
for (int i = 0; i < sortingMethods.length; i++){
System.out.println(sortingMethods[i].getClass().toString());
// Declare the initial array
int array[] = { 9, 8, 10, 3, 4 };
// Show initial array
System.out.print("Initial array: ");
printArray(array);
// Store startTime
double startTime = System.nanoTime();
// Sort the array and show its new state
sortingMethods[i].sort(array);
// Measure method execution time
double endTime = System.nanoTime();
double duration = (endTime - startTime) / 1000000;
System.out.print("Resulting array: ");
printArray(array);
System.out.println("Execution time, ms: " + duration);
System.out.println();
}
}
}
Для компиляции откройте командную строку и перейдите в каталог, в котором находится папка sorting (в ее родительский каталог).
Для компиляции всех файлов запустите команду:
javac sorting/*.java
И наконец, запустите демо:
java sorting.SortingDemo
Результат:
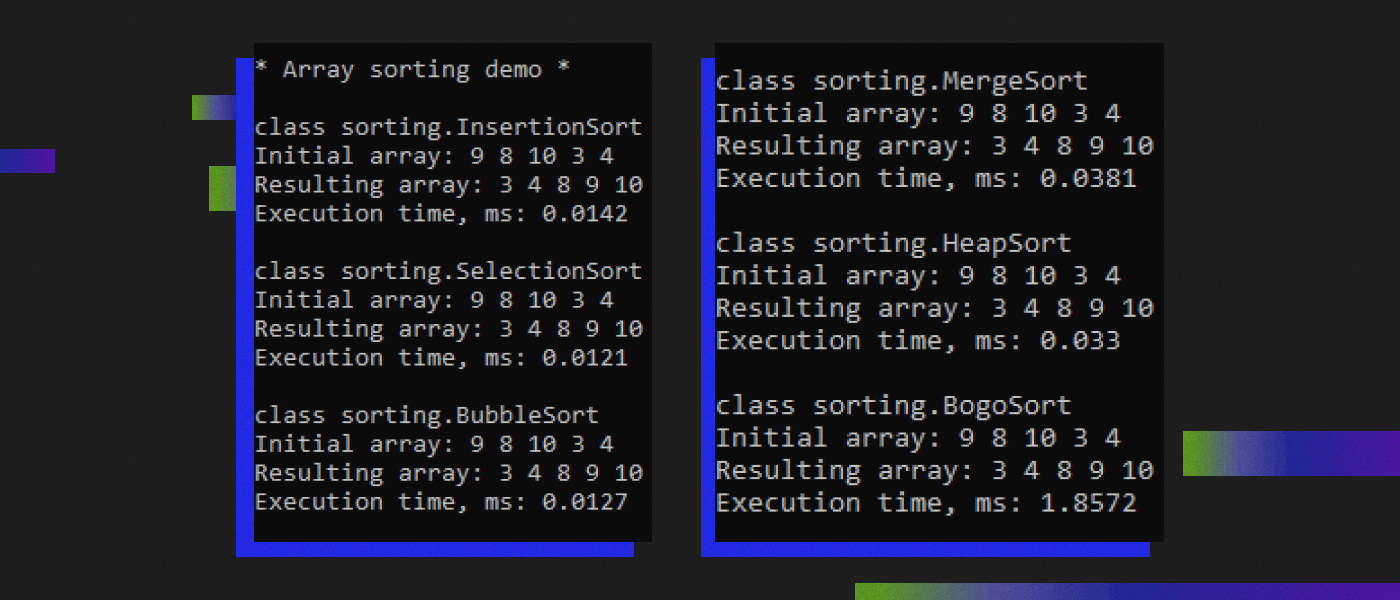
Вторую часть гайда по алгоритмам сортировки на Java от robot_dreams читайте здесь.



