Как математика помогает принимать решения
Конспект вебинара Data Scientist в Airbus.
Сергей Бобровский — Data Scientist в отделении AI Platforms в Airbus и лектор нашего курса «Математика и статистика для Data Science». На своем вебинаре Сергей рассказал, какие подходы к пониманию математики существуют, как эта наука помогает нам в жизни и при чем тут «черный лебедь». Делимся основным.

Что такое математика
Что такое математика? На этот философский вопрос нет простого ответа. Есть четыре ключевых концепции:
#1. Математика — это другой мир
#2. Математика — это логика
#3. Математика — это конструкция, которую создали сами математики
#4. Математика — это игра
Другой мир
Первая концепция — это взгляд философа Платона. Он считал, что математики исследуют другой мир, мир идей. Когда мы доказываем теорему, то ведем себя как первооткрыватели, потому что мир математики уже существует.
Долго считалось, что люди сами открывают двери в другие миры.
Логика
Тенденцией XIX-XX веков стал уход от платонизма. С развитием формальной логики ученые пришли к выводу, что на самом деле математика — это рациональное мышление. Она сводится к логике — исследованию того, как из одних утверждений можно выводить другие. Одним из основателей этого подхода был Бертран Рассел.
Формальная логика гарантирует, что если предпосылки истинны, то финальное утверждение также будет истинным.

Самый известный силлогизм
Но со временем оказалось, что все не так просто.
Рассел считал, что правда предпосылок гарантирует правду последствий. Если мы можем найти все простые аксиомы математики, то способны вывести все результаты с помощью логики. На самом деле оказалось, что не все теоремы можно построить на основе аксиом.
Конструкция
Противниками школы Рассела были интуиционисты (последователи профессора Фридриха Бауэра).
Если платонисты верят, что математики открывают мир, который и без них существует, то приверженцы интуиционизма думают, что сами математики конструируют свои результаты. То есть мы сами создаем правдивые результаты на основе аксиом, и математика — это просто конструкция.
Игра
Один из выдающихся математиков Давид Гильберт считал, что математика — это довольно сложная игра. Математики играют по определенным правилам, оперируя символами (как в настольных играх). Прямой смысл имеет только элементарная арифметика (то, что мы можем посчитать на пальцах). Все остальное — это игровая система, которая закрыта в себе. Если ты играешь по правилам, то всегда придешь к интересным результатам. Но ты свободен делать то, что хочется. Поэтому не нужно вкладывать в математику философию. Математика — это только игра, правила которой мы придумали сами.
Среди современных математиков есть последователи всех четырех школ.
Почему математика важна
Математика есть везде. Весь прогресс, которого мы достигли, стал возможен, потому что мы начали использовать математику.
Американский физик Юджин Вигнер в своей статье «Непостижимая эффективность математики в естественных науках» пытался понять, почему какие-то написанные формулы реально влияют на то, что происходит в мире. Но универсального ответа на этот вопрос нет.
Как же математика моделирует наши отношения? Рассмотрим на примере.
Вы сделали себе горячий кофе и хотели бы добавить молоко, но вам позвонили, и вы не выпили кофе сразу. Вопрос: когда лучше добавить молоко в кофе: сразу или перед тем, как будете пить?
Опишем это математически. Нас интересует температура кофе в каждый момент времени. Мы наблюдаем, что охлаждение зависит от разницы температур. То есть, если оставить жидкость комнатной температуры на столе, она почти не охлаждается. Горячее же охлаждается очень быстро.
Составим дифференциальное уравнение изменения температуры со временем. Решение этого уравнения приводит к экспоненциальному охлаждению.

То есть температура кофе в любой момент времени — это разница между начальной температурой и температурой окружения, и эта температура экспоненциально падает со временем. Когда t стремится к бесконечности, кофе охлаждается до комнатной температуры.
Если я добавлю молоко в начале, температура кофе падает в момент смешивания, я получаю 32,5 градуса. Затем я жду и получаю 24 градуса.
Если я добавлю молоко не сразу, а подожду, то в итоге получу более холодный кофе с молоком — 20 градусов.
Вывод: лучше сразу добавить молоко, если вы не хотите пить холодный кофе.
Известные ошибки мышления
Одна из проблем нашего сознания заключается в том, что мы воспринимаем вероятность как некую неизменную константу, закрепленную за тем или иным исходом. Но на самом деле часто есть смысл думать о вероятности как о степени доверия тому или иному событию, которая может меняться, когда мы узнаем новые факты.
Ошибка выжившего
Когда во время Второй мировой войны решали, какую часть самолета укреплять броней, то исследовали, в какие места уцелевших самолетов чаще попадали снаряды.
Но оказалось, что пробоины — не в тех местах, которые надо укреплять, а в тех, попадание в которые вредит самолету менее всего. Бронировать же нужно те части уцелевших самолетов, где нет ни одного попадания. Потому что все самолеты с отверстиями в этих «белых» местах разбились.
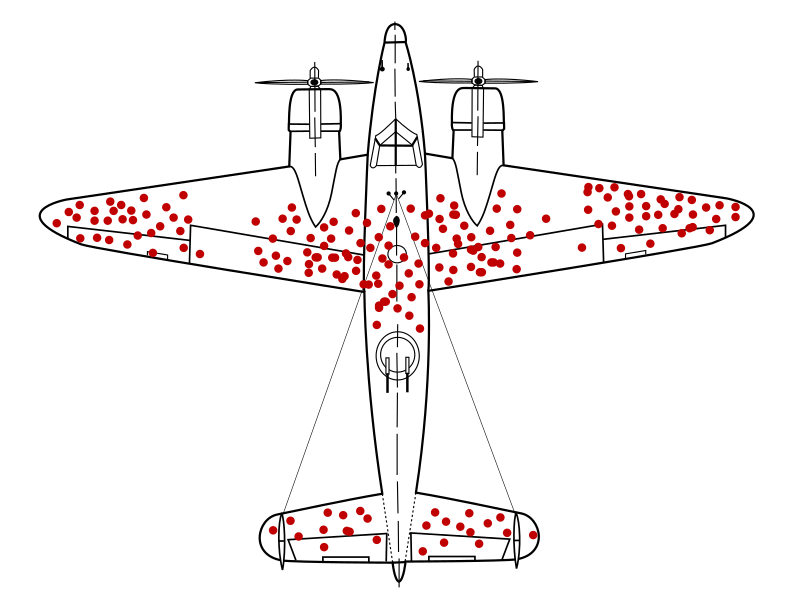
То есть если мы основываем свои решения на данных, полученных от «выживших», то можем прийти к неверным выводам, потому что у нас недостаточно информации о «погибших». Например, мы знаем истории знаменитостей и думаем, что должны вести себя, как они, чтобы достичь успеха. Но есть множество людей, которые делают то же самое, что и успешные, но не добиваются ничего. Однако о них мы знаем недостаточно. Мы видим только траектории победителей.
Ошибка игрока
Если при игре в рулетку много раз подряд выпадает красное, то посетителю казино кажется, что увеличивается вероятность черного (и наоборот). Но на самом деле это не так.
Однажды в Монте-Карло шарик 26 раз подряд попал на черное, и в результате игроки потеряли огромные деньги, потому что уже после 10 бросков были уверены, что должно выпасть красное.
Ошибка базового процента
Если на 2,8 млн людей приходится 100 террористов и есть система их поиска, которая ошибается в 1% случаев, то когда система бьет тревогу, только в 0,3% случаев указанный ею человек действительно будет террористом. Но нам кажется, что 1% погрешности — это очень мало, а значит, система должна быть точной. Такая же ситуация с тестами на заболевания — их точность на самом деле зависит от распространенности заболеваний.
Многие мои примеры связаны с книгой нобелевского лауреата Даниэля Канемана «Думай медленно, решай быстро». Она говорит, что у нас есть две системы принятия решений. Одна — быстрая и автоматическая, нам не нужно напрягаться, чтобы ее задействовать. А для второй, наоборот, нужно сосредотачиваться, проводить вычисления и прикладывать усилия. Часто, когда нам кажется, что мы используем систему 2, на самом деле мы используем систему 1, потому что экономим энергию, внимание и время. Очень часто это правильный подход: он позволяет нам быстро реагировать на окружающие опасности.
Но в современном мире множество опасностей имеют более сложную природу, особенно когда мы говорим о финансовых рисках. Потому важно уметь не доверять самому себе, стараться не останавливаться на решении, которое дает первая система.
Проблему потерь очень легко решать, когда она связана с монетарными потерями. Но если мы свяжем потери с психологией, то окажется, что наша психология потерь не совсем рациональна — мы боимся потерь больше, чем радуемся выигрышам. Из-за этого мы часто пытаемся минимизировать потери, а не максимизировать выигрыш. То есть несколько раз потерять по $10 нам тяжелее, чем один раз выиграть $100.
Советуют иметь собственную политику риска — заранее решить, с какой потерей в среднем я могу жить, и всегда использовать эту политику. Например, никогда не покупать дополнительные страховки. Всегда лучше думать как торговцы ценными бумагами, которые пытаются смотреть на средний выигрыш: you win a few — you lose a few. Главное — выигрывать достаточно часто. Проигрывать иногда — это нормально
Вторая книга, которую я хочу порекомендовать, — «Черный лебедь» Нассима Талеба. Если ее прочесть, может показаться, что она противоречит тому, о чем я тут говорю. Потому что чрезмерное использование математики приводит к иллюзии контроля за событиями.
Представим, что индюк живет на ферме, его кормят каждый день вкусной едой, и он, отталкиваясь от этой информации, рассчитывает, сколько еды получит в будущем. Но не принимает во внимание, что скоро День благодарения, а значит, его зарежут.
То есть все теории имеют свой круг применения и предпосылки. Нечасто, но происходят события, которых мы не ожидаем. Поэтому математику нужно применять очень осторожно и понимать, когда она действует, а когда нет.
Многие примеры, которые я показал, — это примеры простых игр. Они могут увести нас от правильного мышления. Нам не стоит всегда мыслить определенными правилами, которые мы выучили. Концепцию вероятностей нужно воспринимать как степень доверия событию, которое может измениться, и тогда теория вероятностей поможет в принятии решений.
Выводы: как использовать математику при принятии решений
- Будьте очень осторожны, когда принимаете решения, связанные с вероятностями. Наше тело будет советовать быстрые, но часто неправильные решения.
- Уделите время и проанализируйте ситуацию. Используйте математику, в этом вам поможет теорема Байеса.
- Думайте о вероятностях как о степени знания или незнания ситуации. Вероятности могут изменяться после получения новой информации.
- Не обобщайте маленькие выборки. Если у вас есть пример пяти человек, не распространяйте его на всю популяцию.
- Решите для себя, какой уровень риска для вас комфортен, и всегда придерживайтесь его.
- Помните, что даже редкие события иногда случаются.



